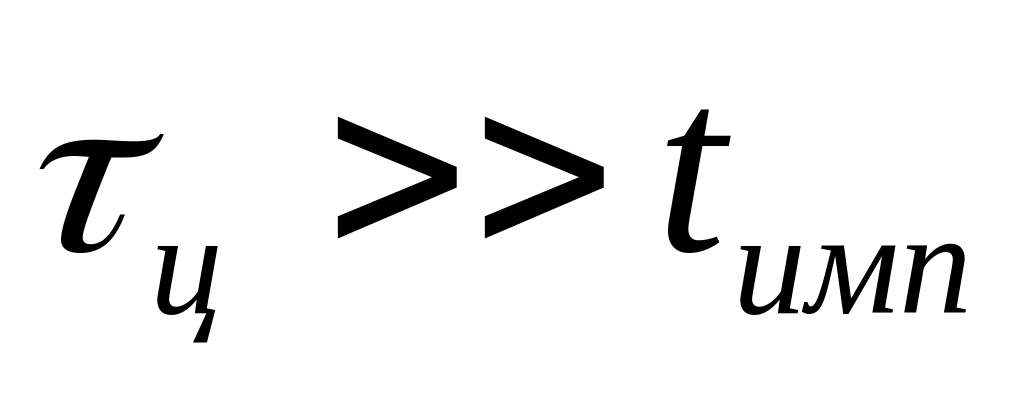6.2.3. Временной метод
Временной метод (метод интеграла наложения, метод интеграла Дюамеля) основан на использовании импульсной h(t ) характеристики цепи, т.е. характеристики цепи во временной области. Импульсная характеристика – это реакция цепи на -функцию. Такой функцией описывается модель сигнала, имеющего бесконечно большую амплитуду, нулевую длительность и площадь, равную 1.
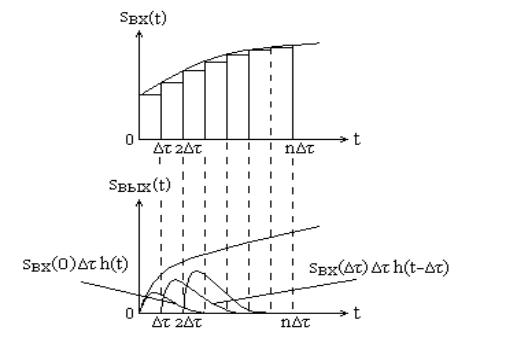
Представим входной сигнал s вх ( t ) сложной формы в виде совокупности прямоугольных импульсов одинаковой и достаточно малой длительности
Реакция цепи в моменты времени k , k 0,1, 2, , n на каждый из этих импульсов (если бы площади их были равны единице) есть импульсная характеристика h ( t k ). Но так как площади импульсов равны s вх ( k ) , то реакция цепи равна s вх ( k ) h ( t k t ). В свою очередь выходной сигнал в некоторый момент времени t k будет равен сумме реакций цепи на импульсы в интервале 0 t , т.е.
s вых ( t ) s вх ( k ) h ( t k ).
При 0 суммирование сводится к операции интегрирования по переменной k :
Рис. 6.2. Свертка сигнала с импульсной характеристикой
Таким образом, значения выходного сигнала линейной цепи в любой момент времени являются результатом взвешенного суммирования мгновенных значений входного сигнала. Весовая функция – это импульсная характеристика цепи.
Учитывая, что для реальных цепей h ( t ) 0 при t 0, можно записать
s вых ( t ) s вх ( ) h ( t ) d s вх ( t ) h ( t ).
Полученное выражение для s вых ( t ) представляет собой интеграл наложения, или интеграл Дюамеля. В математике полученное выражение называют сверткой двух функций. Таким образом, выходной сигнал линейной цепи равен свертке входного сигнала и импульсной характеристики цепи.
Иногда используют другую форму записи интеграла Дюамеля, которую
можно получить путем замены переменной
Заметим, что интеграл Дюамеля
можно получить из формулы
S вых ( j ) S вх ( j ) K ( j ), на которой основан спектральный метод анализа цепей. Для этого воспользуемся свойствами преобразования Фурье и связью между частотной и импульсной характеристиками цепи, имея в виду, что частотная характеристика K ( j ) цепи является по существу спектральной плотностью ее импульсной характеристики h ( t ).
Источник
7.5. Временной метод анализа переходных процессов
В теории цепей данный метод (интеграл наложения) применяется для цепей с нулевыми начальными условиями, т.к. в методе используются импульсные или переходные характеристики линейных цепей, введенные для нулевых начальных условий. В интегральной форме записи метод применяется со входными сигналами (подключаемыми к цепи), которые можно задать аналитически. В случае, если входной сигнал невозможно задать аналитически, интеграл заменяется суммой.
В анализе используются две формы интеграла наложения с переходной характеристикой и с импульсной характеристикой.
Интегралы наложения, например, для напряжения:
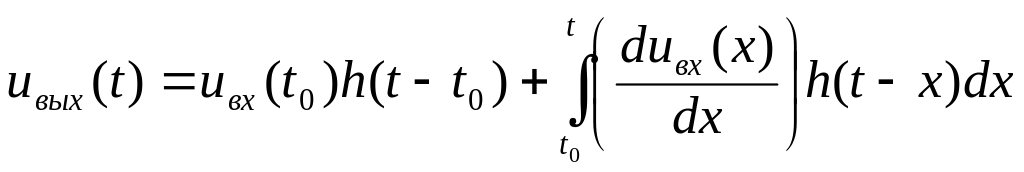
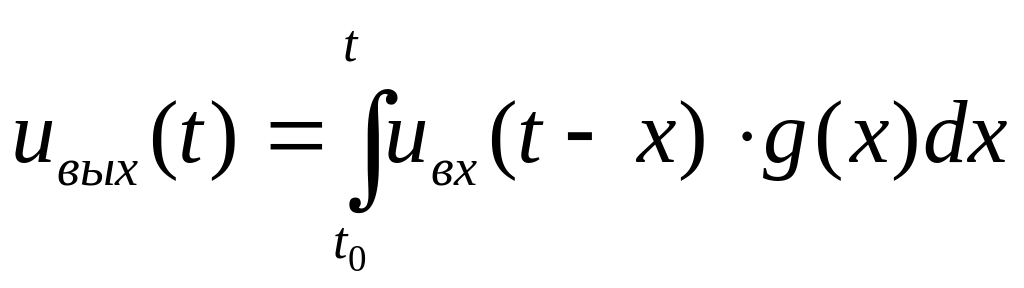
Выражения (7.21), (7.22) получены следующим образом. По определению, переходная характеристика h(t) — это отношение переходного процесса от включения на линейную цепь с нулевыми начальными условиями постоянного напряжения (неединичного скачка) к величине этого напряжения.
Импульсная характеристика g(t) — это отношение переходного процесса от включения на линейную цепь с нулевыми начальными условиями импульса неединичной площади к площади этого импульса.
Произвольный входной сигнал может быть представлен суммой «скачков» или »импульсов» (динамическое представление сигнала), а затем , используя определения h(t) и g(t) и предельный переход, получают выражения (7.21), (7.22).
Пример 9. Используя схему (рис. 7.1), условие задачи и выражения (7.10) для импульсной характеристики 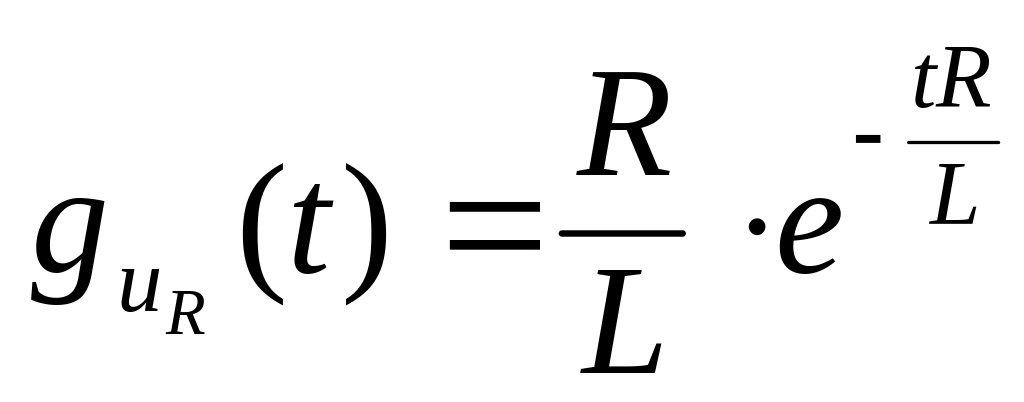
Решение. Согласно выражению (7.22):
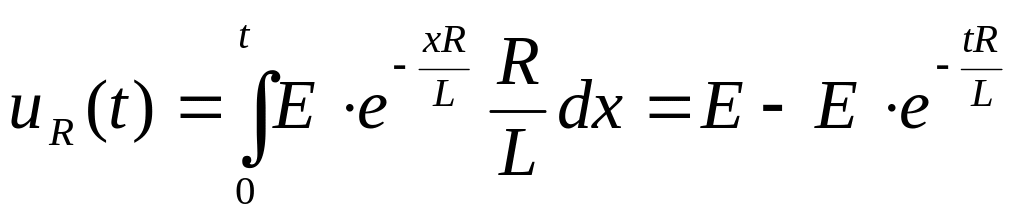
7.6 Дифференцирование и интегрирование сигналов электрическими цепями
Переходные процессы в линейных электрических цепях в некоторых случаях похожи на результаты дифференцирования и интегрирования входного импульсного воздействия (см. например, рис. 7.2). Целесообразно рассмотреть условия, удовлетворяющие этим операциям. Рассмотрим, например, эквивалентную схему (рис 7.7), с произвольным входным сигналом.
Пусть выходное напряжение снимается с ёмкости ( 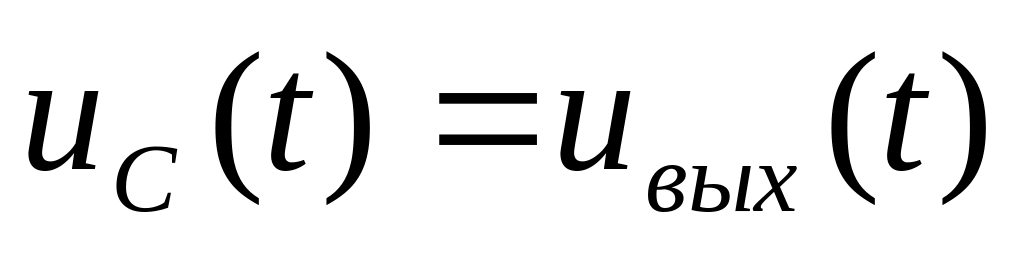
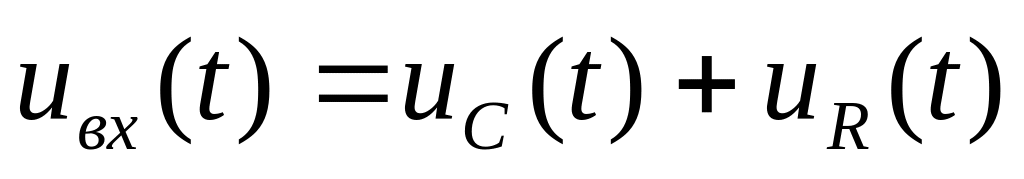
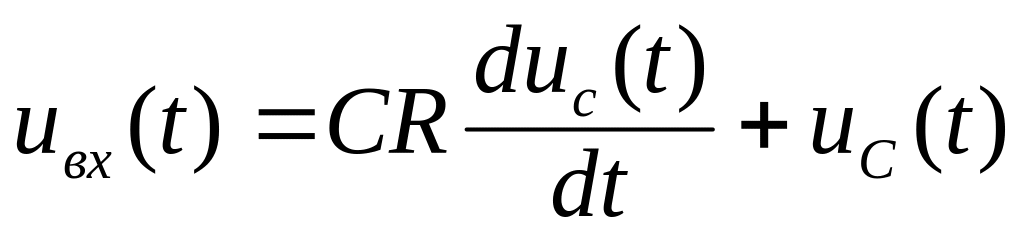
Постоянная ц=RC для данной схемы называется постоянной времени цепи. При 
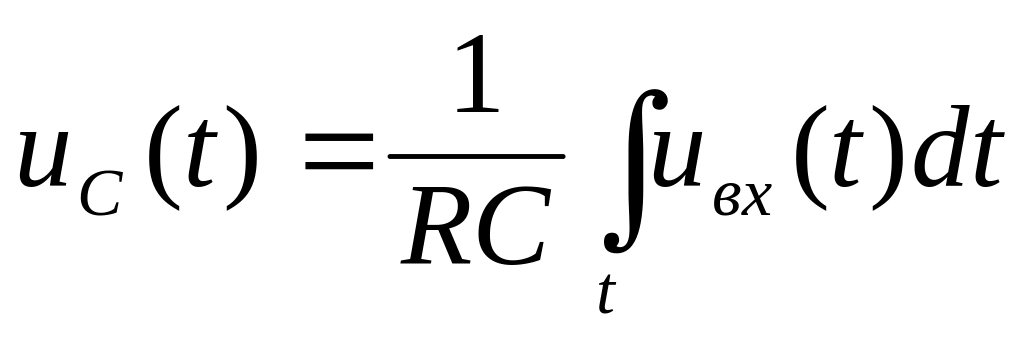
Аналогично, при »снятии» выходного напряжения с сопротивления и при , происходит дифференцирование входного сигнала.
7.7 Контрольные задания
а) объяснить принципы непрерывности и законы коммутации;
б) классическим методом провести анализ переходных процессов примера 7.2. Значения элементов и напряжение источника сигнала выбрать самостоятельно;
в) объяснить принцип анализа переходных процессов частотным методом;
г) провести анализ переходных процессов при нулевых начальных условиях схемы (рис. 7.7) операторным методом при включении постоянного источника напряжения. Значения элементов и напряжение источника сигнала выбрать самостоятельно;
д) объяснить принцип анализа переходных процессов с помощью интегралов наложения;
е) обосновать условия дифференцирования и интегрирования для схемы (рис. 1.1.)
Источник
Временные методы анализа переходных процессов
В ряде электронных схем по принципу действия на цепи воздействуют импульсы напряжения или
тока, отличные от нуля лишь в течение некоторого короткого интервала времени. Рассмотрим способы
определения переходных процессов в цепях при таких воздействиях.
Пусть задан импульс, форма которого изображена на рис. 1. Площадь под кривой, ограничиваю-
Предположим теперь, что длительность импульса устремляется к 0, а его площадь остается неиз-
менной и равной 1. Тогда функция δ(t,t и ) в пределе будет равна всюду, кроме момента времени t=0+
нулю, а в этот момент обращается в бесконечность, сохраняя площадь, равную 1. При этом функцию
δ(t) называют единичной импульсной функцией, или функцией Дирака. Можно себе представить им-
пульсную функцию площадью, отличной от 1 и равной, например, S и , как S и δ(t) .
Таким образом, из сказанного следует выполнение условия:
∞ ∫ δ ( t ) dt = 1 , где функция δ(t)=0 при t≠0.
Воздействие δ -функции на систему называется единичным импульсным воздействием. Если воз-
действует функция S и δ(t) , то это импульсное воздействие.
Рассмотрим вначале реакции простейших цепей на импульсное воздействие (рис. 3.13).
Т.е. энергия, сообщаемая емкости равна:
Аналогично для индуктивности
Т.е. системе мгновенно сообщается заданная энергия. Таким образом, мощность в цепи бесконеч-
В ряде случаев необходимо знать реакцию системы на такого рода воздействие. Например если
τ>>t и (где τ — постоянные времени схемы RC , L/R , 2 π 
ложено импульсное воздействие: радиосхемы например.
Реакция цепи на импульсное воздействие — импульсная реакция или импульсная характеристика
Удобнее всего находить реакцию операторным методом. Для этого найдем изображение δ(t) .
Здесь подынтегральное выражение только в момент времени t=0 отлично от нуля. С другой стороны е -pt =1 при t=0, следовательно, из геометрического смысла определенного интеграла ∆(p)=1 . Если действует S и δ(t) , то изображение такой функции будет S и :
Тогда, если передаточная функция системы H(p) , то изображение реакции ее на импульсное воздействие F 2 (p):
В случае единичного импульсного воздействия F 2 (p)=1 H(p)=H(p). Т. е. импульсная характеристика
системы g(t) ÷ H(p) . Это очень важное свойство, которое позволяет считать импульсные характеристики систем.
Рассмотрим импульсную реакцию интегрирующей RC-цепи (см. рис. 3.14) при нулевых начальных условиях. Отметим, что импульсную реакцию схемы можно находить а) операторным методом, зная изображение по Лапласу для входного воздействия, и б) с помощью операторной передаточной функции. Результирующие выражения:
Источник