Маршруты, цепи, циклы
До 4 баллов за конспект
Определение. Маршрутом называют последовательность вершин и ребер, в которой любые два соседних элемента инцидентны.
В случае простого графа маршрут однозначно определяется последовательностью вершин или последовательностью ребер. Если маршрут в простом графе задан последовательностью вершин v 0, v 1 ,, …, vk, то вершины v 0, vk называют концами маршрута. Если v 0 = vk, то маршрут называют замкнутым, в противном случае – незамкнутым.
Определение. Маршрут, в котором нет повторений ребер, называется цепью. Цепь, в которой все вершины различны, кроме, может быть, ее концов называется простой. Замкнутая простая цепь называется простымциклом. Про цепь говорят, что она соединяет свои концы.
Определение. Простой цикл с р вершинами обозначается Ср . Например, граф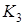 
– это одновременно граф С3.
Определение. Ориентированная простая цепь называется путем, ориентированный простой цикл называют контуром.
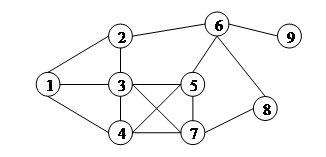
Рассмотрим граф на рис. 11. Маршруты в этом графе будем задавать последовательностью вершин.
Пример маршрута: 1 – 2 – 3 – 5 – 7 – 4 – 3 – 5 – 6 – 2 – 3 – 4.
Пример замкнутого маршрута: 3 – 4 – 5 – 7 – 3 – 4 – 1 – 3.
Пример цепи, соединяющий вершины 6 и 8: 6 – 5 – 3 – 4 – 5 – 7 – 3 – 2 – 6 – 8.
Пример цикла: 5 – 3 – 2 – 6 – 5 – 7 – 4 – 5.
Примеры простых цепей, соединяющих вершины 1 и 6: 1 – 3 – 4 – 5 – 6; 1 – 2 – 6; 1 – 4 – 7 – 8 – 6.
Примеры простых циклов: 3 – 5 – 7 – 4 – 3; 1 – 2 – 6 – 8 – 7 – 4 – 1;
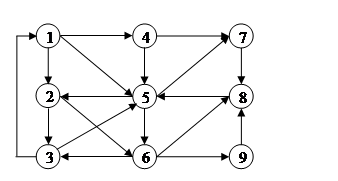
Рассмотрим ориентированный граф на рис. 12. Ориентированные маршруты в этом графе будем задавать последовательностью вершин, проходимых в направлении ориентации дуг.
Пример ориентированного маршрута: 1 ® 2 ® 3 ® 5 ® 2 ® 6 ® 8 ® 5.
Пример замкнутого ориентированного маршрута: 1 ® 4 ® 5 ® 2 ® 6 ® 8 ® 5 ® 2 ® 3 ® 1.
Пример ориентированной цепи: 4 ® 5 ® 7 ® 8 ®5 ® 2.
Пример замкнутой ориентированной цепи: 6 ® 8 ® 5 ® 2 ® 3 ® 1 ® 5 ® 6.
Пример пути, соединяющего вершины 3 и 9: 3 ® 1 ® 4 ® 5® 6 ® 9.
Пример контура: 5 ® 7 ® 4 ® 5.
Определение. Длиной маршрута называют число ребер в нем с учетом повторений.
Определение. Расстоянием между вершинами называют длину кратчайшей цепи, соединяющей эти вершины. Сама такая цепь называется геодезической.
Определение. Самая длинная геодезическая цепь называется диаметром графа. Длину диаметра так же будем называть диаметром и обозначать буквой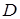 
. Расстояние между вершинами и и v обозначим через d (u, v).
Рассмотрим граф на рис. 11.
d (1, 5) = 2; d (5, 7) = 1; d (4, 9) = 3; d (1, 8) = 3. 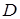= 3 и геодезических длины 3 в графе несколько. Например, это геодезические 1 – 2 – 6 – 9 и 1 – 4 – 7 – 8.
Определение. Ярусом вершины v порядка n (обозначение: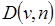 
), n = 0, 1, 2, … называется множество вершин, находящихся от вершины v на расстоянии n.
Рассмотрим граф на рис.11 и выпишем ярусы вершины 9.
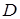
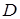
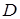
D (9, 0) = <9>; (9, 1) = <6>; (9, 2) = <2, 5, 8>; (9, 3) = <1, 3, 4, 7>.
Определение. Две вершины и и v называются связными, если их соединяет хотя бы одна простая цепь.
Очевидно, что отношение связности — это отношение эквивалентности.
Определение. Граф G (V, E) называют связным, если любые две его вершины можно соединить простой цепью. В противном случае граф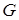 
называется несвязным.
Несвязный граф состоит из нескольких связных компонент связности. Вершины, входящие в некоторую компонентусвязности образуют класс эквивалентности по отношению связности.
На рис. 13 показан граф, состоящий из четных компонент связности.
Определение. Ориентированный граф называется сильно связным, если любые две его вершины можно соединить путем. Ориентированный граф называется слабо связным, если связен граф, получающийся из данного орграфа заменой всех дуг на ребра. На рис. 14 показаны сильно связный и слабо связный орграфы.
В заключение опишем необходимые и достаточные условия двудольности графа.
Утверждение (Кениг). Граф является двудольным тогда и только тогда, когда все его простые циклы имеют четную длину.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Источник
5.1.2. Некоторые виды графов
Определение. Граф такой, что любые две его вершины смежны, называется полным графом. Полный граф с р вершинами обозначается 
. На рис. 6 показаны графы 
.
Степень каждой вершины графа Кр равна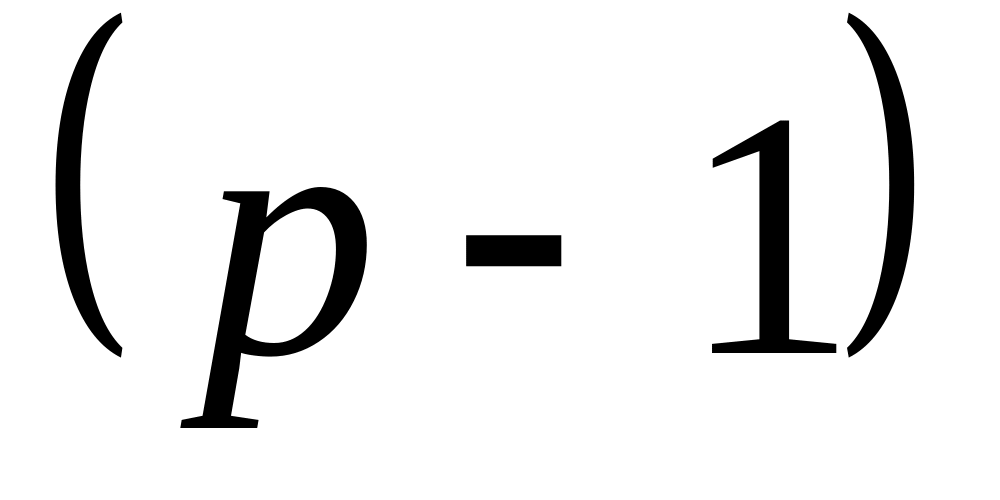 
. Следовательно, число ребер графа Кр равно 
.
Определение. Граф называется регулярным степени k, если все его вершины имеют одну и туже степень k. На рис. 7 приведены примеры регулярных графов степени 3. Всякий полный граф Кр – это регулярный граф степени .
Определение. Граф с пустым множеством ребер называется вполне несвязным графом. Вполне несвязный граф с р вершинами будем обозначать через Np. Граф N1, состоящий из единственной вершины, называется тривиальным графом.
5.1.4. Маршруты, цепи, циклы
Определение. Маршрутом называют последовательность вершин и ребер, в которой любые два соседних элемента инцидентны.
В случае простого графа маршрут однозначно определяется последовательностью вершин или последовательностью ребер. Если маршрут в простом графе задан последовательностью вершин v0, v1,, … , vk, то вершины v0, vk называют концами маршрута. Если v0 = vk, то маршрут называют замкнутым, в противном случае – незамкнутым.
Определение. Маршрут, в котором нет повторений ребер, называется цепью. Цепь, в которой все вершины различны, кроме, может быть, ее концов называется простой. Замкнутая простая цепь называется простым циклом. Про цепь говорят, что она соединяет свои концы.
Определение. Простой цикл с р вершинами обозначается Ср . Например, граф – это одновременно граф с3.
Определение. Ориентированная простая цепь называется путем, ориентированный простой цикл называют контуром.
Рассмотрим граф на рис. 11. Маршруты в этом графе будем задавать последовательностью вершин.
Пример маршрута: 1 – 2 – 3 – 5 – 7 – 4 – 3 – 5 – 6 – 2 – 3 – 4.
Пример замкнутого маршрута: 3 – 4 – 5 – 7 – 3 – 4 – 1 – 3.
Пример цепи, соединяющий вершины 6 и 8: 6 – 5 – 3 – 4 – 5 – 7 – 3 – 2 – 6 – 8.
Пример цикла: 5 – 3 – 2 – 6 – 5 – 7 – 4 – 5.
Примеры простых цепей, соединяющих вершины 1 и 6: 1 – 3 – 4 – 5 – 6; 1 – 2 – 6; 1 – 4 – 7 – 8 – 6.
Примеры простых циклов: 3 – 5 – 7 – 4 – 3; 1 – 2 – 6 – 8 – 7 – 4 – 1;
Рассмотрим ориентированный граф на рис. 12. Ориентированные маршруты в этом графе будем задавать последовательностью вершин, проходимых в направлении ориентации дуг.
Пример ориентированного маршрута: 1 2 3 5 2 6 8 5.
Пример замкнутого ориентированного маршрута: 1 4 5 2 6 8 5 2 3 1.
Пример ориентированной цепи: 4 5 7 8 5 2.
Пример замкнутой ориентированной цепи: 6 8 5 2 3 1 5 6.
Пример пути, соединяющего вершины 3 и 9: 3 1 4 5 6 9.
Пример контура: 5 7 4 5.
5.2.2. Матрица смежности графа
Матрица смежности неориентированного графа.
Определение. Матрицей смежности неориентированного графа 
называется квадратная матрица с р строками и с р столбцами. Элементы матрицы определяются правилом:
Матрицу смежности обозначим буквой А.
Пример графа и его матрицы смежности показан на рис. 9.
Источник