Цепь маркова предельные вероятности состояний

Лекция № 2. Цепи маркова

1. Марковские случайные процессы

Среди случайных процессов важную роль играют марковские, названные по фамилии А.А. Маркова 4 , российского математика (1856-1922), который впервые начал их изучать. Особенность марковских процессов – отсутствие последействия (состояние системы в будущем полностью определяется ее состоянием и параметрами в настоящий момент времени), что позволяет достаточно просто описывать такие процессы.

Марковские процессы широко применяются при изучении автоматизированных систем управления, при моделировании работы различных технических устройств, систем массового обслуживания, а также в биологии, экономике и других областях знания.

Рассмотрим некоторую физическую систему S, которая может изменять свои состояния. Состояний у системы S может быть конечное или счетное число, тогда систему называют системой с дискретными состояниями. Пусть в системе S протекает случайный процесс следующего вида: система S может находиться в одном из состояний 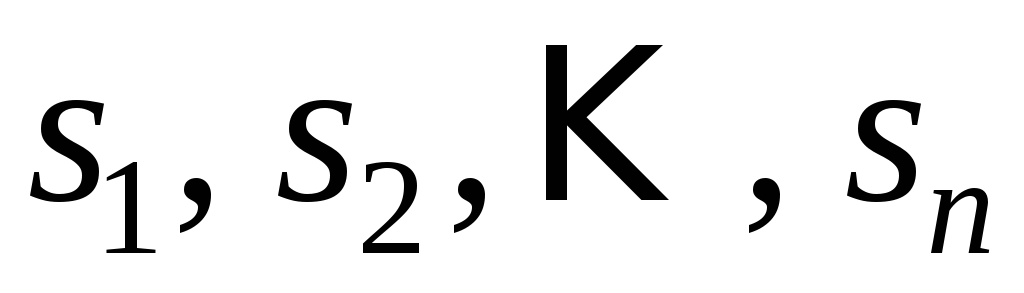и под действием случайных причин с течением времени переходить из одного состояния в другое. Такой случайный процесс называют дискретным случайным процессом.

Такой случайный процесс с точки зрения его структуры изображают с помощью графа состояний. Граф состояний – ориентированный граф, вершины графа (прямоугольники) соответствуют состояниям системы, ориентированные пути (стрелки) 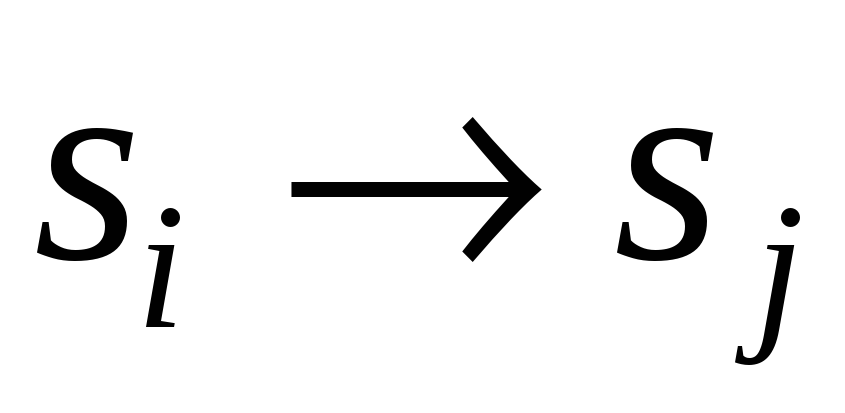обозначают возможность перехода системы из состояния в состояние непосредственно, минуя другие состояния. Рассматривают также стрелки , обозначающие задержку в . Предполагается, что переходы из состояния в состояние происходят мгновенно.

Важнейшими характеристиками системы с дискретными состояниями являются вероятности состояний.

Определение 1. Вероятностью i-го состояния в момент времени t называется вероятность события, состоящего в том, что в момент t система S будет в состоянии .

(1)

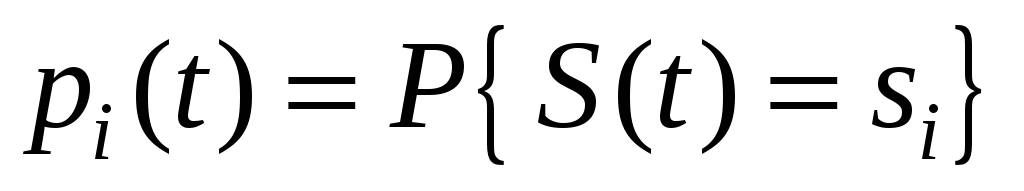
В любой момент времени сумма вероятностей всех состояний равна 1.

(2)

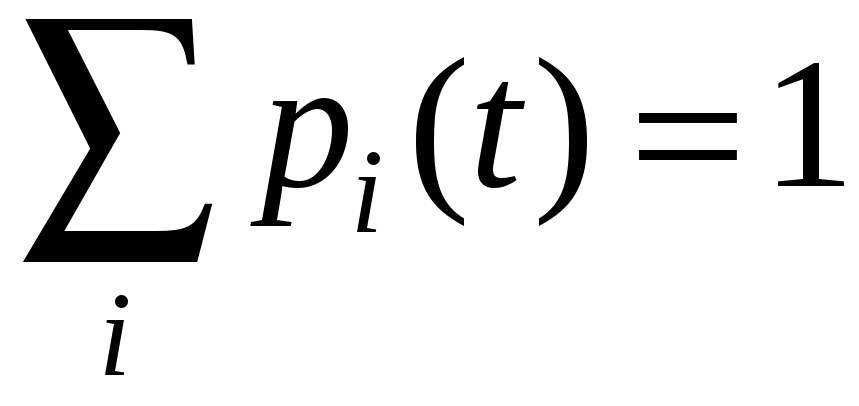
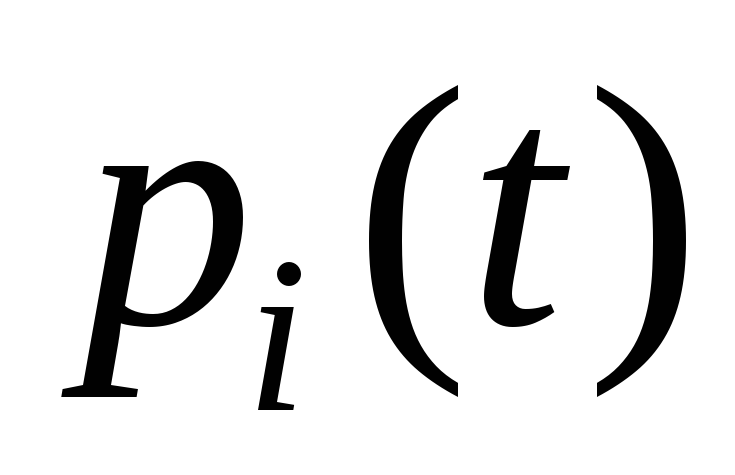
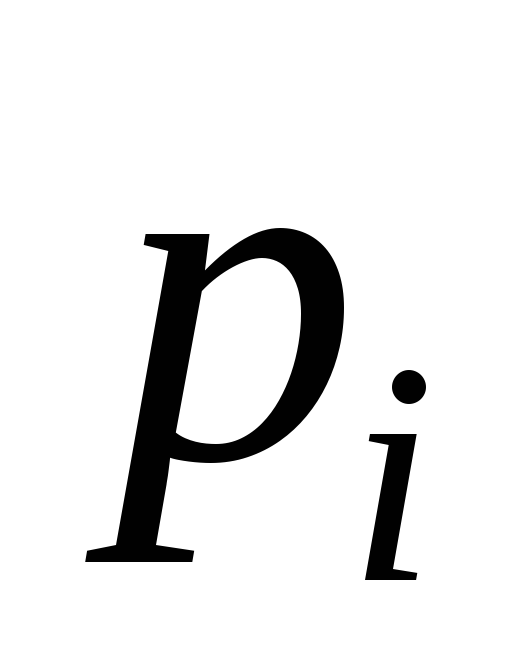
Во многих практических вопросах нас интересует стационарный режим, который устанавливается, когда от начала процесса проходит достаточно много времени. При этом состояния системы хотя и меняются случайным образом, но их вероятности остаются практически неизменными. Обозначим эти постоянные вероятности :

.

Определение 2. Вероятности 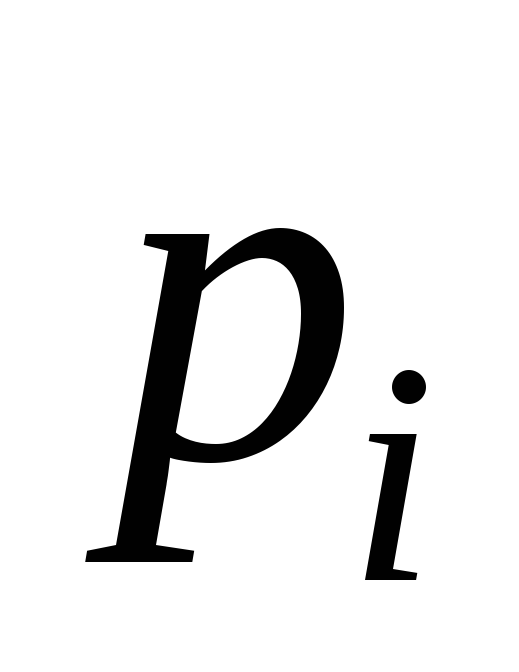, если они существуют, называются предельными вероятностями состояний.

Соответственно, для процессов с дискретными состояниями рассматриваются 2 основные задачи:

Найти вероятности состояний в любой момент времени t.

Найти предельные вероятности состояний (если они существуют).

Наиболее просто эти задачи решаются для марковских случайных процессов.

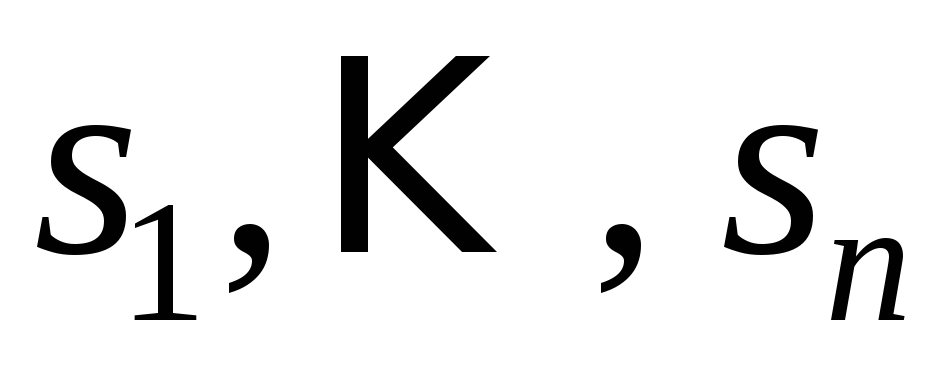
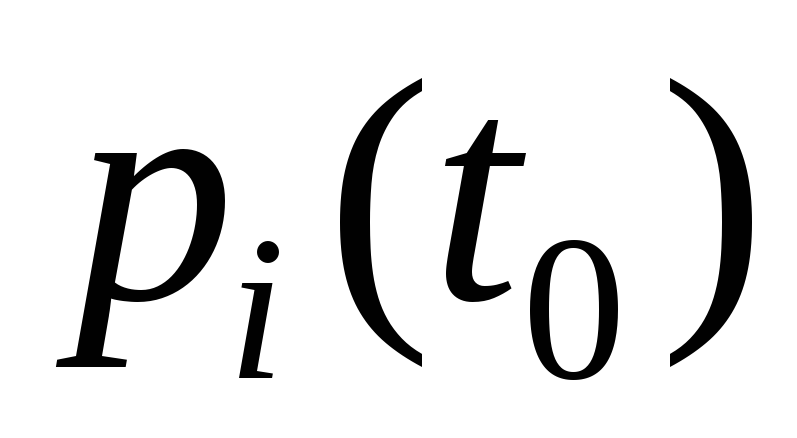
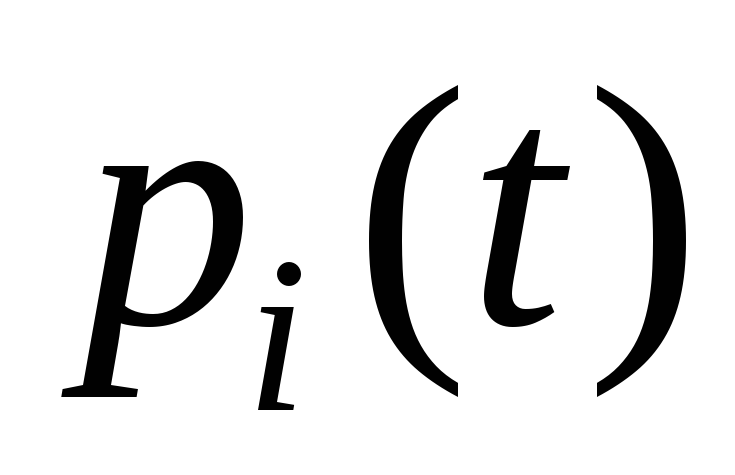
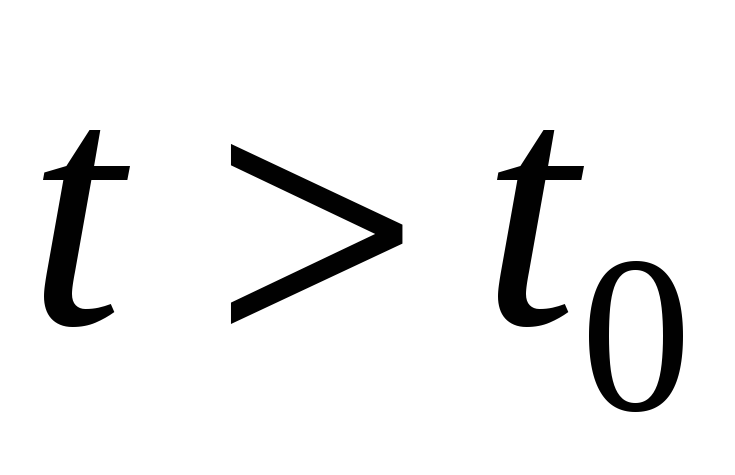
Определение 3. Случайный процесс, протекающий в системе с дискретными состояниями , называется марковским, если, зная вероятности состояний (в настоящем), можно определить при (в будущем), и при этом не важно, как система «приходит» в эти состояния.

Данное определение не означает, что на будущее не оказывает влияние прошлое системы: будущее зависит от прошлого через настоящее. Идея марковского процесса заимствована из классической механики, где состояние системы в ближайшем будущем определяется заданием координат и скоростей в начальный момент времени, и не имеет значения, какими они были до этого.

Источник

Классификация цепей Маркова. Основные определения, понятия, характеристики.

Состояние Ej достижимо из состояния Ei, если найдется такое число шагов m0, что вероятность перехода из i в j за m0 шагов >0 ( Pij(m0)>0 ).

Если Ej достижимо из Ei и Ei достижимо из Ej, то состояние – сообщающееся.

Дискретная цепь Маркова называется неприводимой, если все ее состояния сообщающиеся.

Замкнутое подмножество: Пусть А – множество всех возможных состояний цепи Маркова. Имеем два подмножества: A1 и A1c (дополнение подмножества A1). Тогда подмножество A1 – замкнутое, если состояние подмножества А1с недостижимо из состояния подмножества А1. Если же при этом А1 состоит из одного состояния Ej, то оно называется поглощающим состоянием.

Необходимым и достаточным условием наличия поглощающего состояния является Eij = 1.

Если подмножество А1 замкнутое и не содержит никакого другого замкнутого подмножества, то получается неприводимая цепь Маркова. Подмножество B – неприводимое. С другой стороны, если подмножество А1 замкнуто и не содержит собственные замкнутые подмножества, то цепь Маркова – приводимая.

Характеристики состояний и их свойства – см. лекции.

P [Вероятность того, что первое возвращение в состояние Ej произойдет через n шагов после ухода из этого состояния] => fj – вероятность того, что мы когда-нибудь вернемся в это состояние.

Это свойство дает возможность проклассифицировать дискретные цепи Маркова.

Если fj = 1, то Ej – возвратное состояние, а если fj 3 / 7 34567> Следующая >>>

Источник

25. Цепь Маркова. Матрица вероятностей переходов. Однородная цепь Маркова. Предельные вероятности состояний. Марковский процесс с дискретными состояниями и непрерывным временем.

Марковский процесс — протекающий в системе случайный процесс, который обладает свойством: для каждого момента времени t₀ вероятность любого состояния системы в будущем (при t>t₀) зависит только от ее состояния в настоящем (при t= t₀) и не зависит от того, когда и каким образом система пришла в это состояние (т.е. как развивался процесс в прошлом).

Наиболее простым процессом является цепь Маркова – марковский случайный процесс с дискретным временем и дискретным конечным множеством состояний.

Переходные матрицы обладают свойством:

— все их элементы неотрицательны;

— их суммы по строкам равны единице.

Матрицы с таким свойством называют стохастическими.

Матрицы переходов позволяют вычислить вероятность любой траектории цепи Маркова с помощью теоремы умножения вероятностей.

Для однородных цепей Маркова матрицы переходов не зависят от времени.

Марковский процесс называется однородным, если вероятности перехода за единицу времени не зависят от того, где на оси времени происходит переход.

Пределы вероятностей р₁(m), р₂(m),…, р_n(m) при m→∞, если они существуют, называются предельными вероятностями состояний.

Марковский процесс с дискретными состояниями и непрерывным временем.

-примеры: выход из строя любого элемента аппаратуры может произойти в любой момент времени, окончание ремонта этого элемента также может произойти в произвольный момент и т.д.

Для описания таких процессов может быть применена схема Марковского случайного процесса с дискретными состояниями и непрерывным временем.

Для вероятностей состояний p(t) такого процесса выполнено:

,

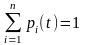
т.к. в момент времени t система находится в одном из своих состояний.

В случае процесса с непрерывным временем, вероятность перехода системы из состояния в состояние точно в момент t будет равна нулю так же, как вероятность любого отдельного значения случайной непрерывной величины. Поэтому вместо переходных вероятностей p_ij рассматривают плотности вероятностей перехода.

26. Генеральная и выборочная совокупности. Повторная и бесповторная выборки. Репрезентативная выборка. Способы отбора.

Генеральной совокупностью называется совокупность объектов, из которых производится выборка.

Выборочной совокупностью (выборкой) называется совокупность случайно отобранных объектов.

Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.

Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.

Для того чтобы по данным выборки можно было достаточно уверенно судить об интересующем признаке генеральной совокупности, необходимо, чтобы выборка правильно представляла пропорции генеральной совокупности. Это требование кратко формулируют так: выборка должна быть репрезентативной (представительной).

Принципиально делятся на два вида:

Отбор, не требующий расчленения генеральной совокупности на части. Сюда относятся:

а) простой случайный бесповторный отбор;

б) простой случайный повторный отбор (объекты извлекают по одному из всей генеральной совокупности).

Отбор, при котором генеральная совокупность разбивается на части. Сюда относятся:

На практике часто применяют комбинированный отбор.

Источник