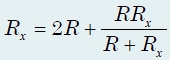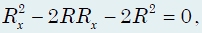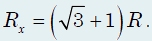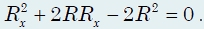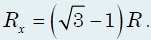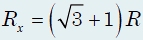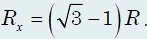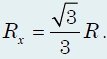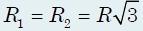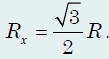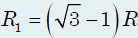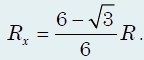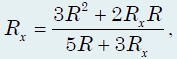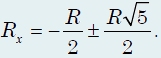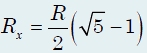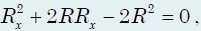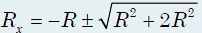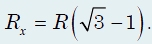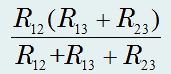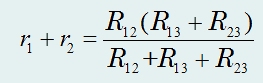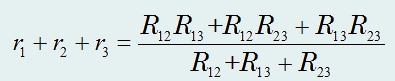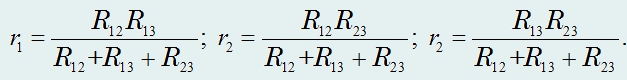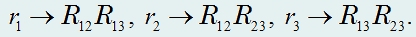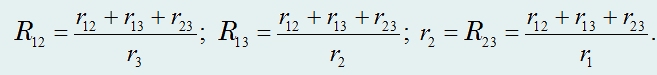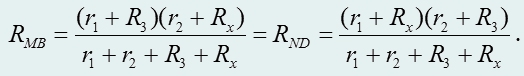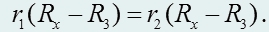Расчет эквивалентных сопротивлений линейных бесконечных цепей



Особую группу образуют задачи на расчет эквивалентных сопротивлений бесконечных цепей. Как правило, эти цепи симметричны и во многих случаях содержат одинаковые элементы (резисторы). Рассматриваемые задачи можно разбить на три группы:
а) линейные (одномерные);
б) плоскостные (двумерные);
в) объемные (трехмерные).
Эвристические приемы решения подобных задач просты и достаточно оригинальны. Причем последние два типа задач решаются только с помощью искусственного приема, содержание которого будет рассмотрено ниже.
Найдем эквивалентное сопротивление типичной линейной бесконечной цепи резисторов, состоящей из повторяющихся элементов (секций), в типичной задаче.
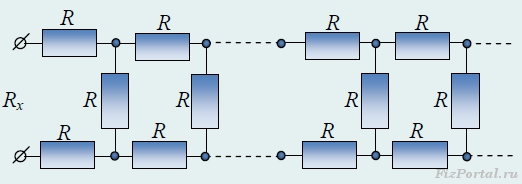
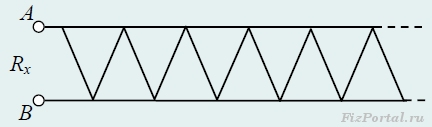
Задача 1. Найдите эквивалентное сопротивление бесконечной цепочки (рис.), которая состоит из одинаковых резисторов сопротивлением R каждый.
Решение (типовое, алгоритм).
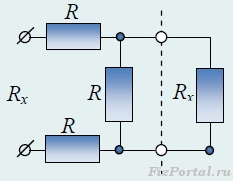
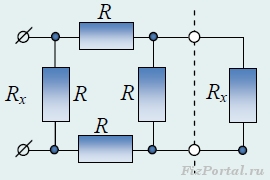
Для нахождения эквивалентного сопротивления цепи необходимо выделить общую секцию, которая бесконечно повторяется. Вполне очевидно, что если отделить ее от цепи, то общее сопротивление этой цепи не изменится, т.к. число элементов (секций) бесконечно. В силу вышесказанного, выделив повторяющуюся секцию в цепи и заменив сопротивление, остальной цепи искомым сопротивлением Rх, получим эквивалентную схему (рис.).
Найдем сопротивление цепи, предварительно записав выражение для Rх через Rx. Опуская промежуточные выкладки, получим:
Рассмотрим еще одну подобную задачу.
Задача 2. Найдите эквивалентное сопротивление бесконечной цепочки (рис.), которая состоит из одинаковых резисторов сопротивлением R каждый.
Решение.
Применим точно такой же прием, но с другой повторяющейся секцией (рис.).
После аналогичных расчетов получим:
Отсюда легко записать ответ:
Можно сформулировать более сложные задачи, решение которых сводится к рассмотренным выше алгоритмам.
Задача 3. Найдите эквивалентное сопротивление между точками А и В бесконечной цепочки (рис.), которая состоит из одинаковых резисторов сопротивлением R каждый.
Решение.
Эквивалентное сопротивление цепи равно сопротивлению двух одинаковых и параллельно соединенных резисторов, сопротивления которых равны (см. решения задач 1 и 2):
справа
Тогда после простых расчетов легко получить ответ:
Задача 4. Найдите эквивалентное сопротивление между точками А и В бесконечной цепочки (рис.), которая состоит из одинаковых резисторов сопротивлением R каждый.
Решение.
Эквивалентное сопротивление цепи равно сопротивлению двух одинаковых и параллельно соединенных резисторов сопротивлением
каждый (см. решение задачи 2).
Отсюда легко получить ответ:
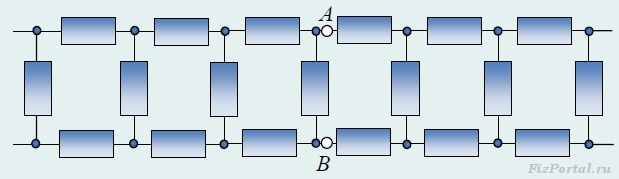
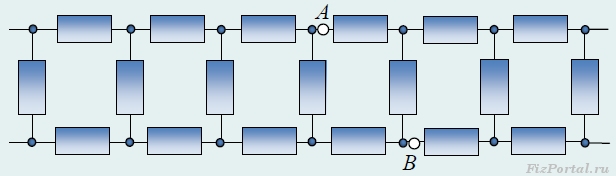
Задача 5. Найдите эквивалентное сопротивление между точками А и В бесконечной цепочки (рис.), которая состоит из одинаковых резисторов сопротивлением R каждый.
Решение.
Эквивалентное сопротивление цепи равно сопротивлению четырех резисторов, соединенных между собой в цепь, которая изображена на рисунке.
(см. решения задач 1 и 2). Отсюда искомое эквивалентное сопротивление цепи между точками А и В:
Задача 6. Найдите эквивалентное сопротивление между точками А и В бесконечной цепочки (рис.), которая состоит из одинаковых проволочных резисторов сопротивлением R каждый.
Решение.
Эквивалентная схема представлена на рисунке.
Повторяющаяся секция состоит из четырех резисторов. Полное сопротивление цепи находим, полагая RAB= Rх.
Опуская промежуточные выкладки, получим
Второй корень уравнения отрицательный и не имеет смысла. Окончательный результат:
Рассмотрим более трудную задачу, решение которой предполагает предварительное использование метода исключения пассивных элементов цепи.
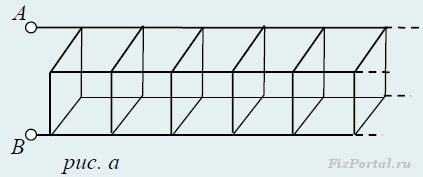
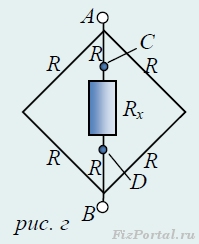
Задача 7. Найти эквивалентное сопротивление между точками А и В бесконечной цепочки (рис. а), которая состоит из одинаковых проволочных резисторов сопротивлением R каждый.
Решение.
Чтобы найти эквивалентное сопротивление цепи, необходимо сначала выделить общую секцию, которая бесконечно повторяется. Понятно, что если отделить ее от цепи, то общее сопротивление этой цепи не изменится. Выделить повторяющуюся секцию в рассматриваемой цепи можно, но заменить сопротивление остальной части цепи искомым сопротивлением Rх нельзя, т.к. оставшаяся часть имеет четыре соединительных провода.
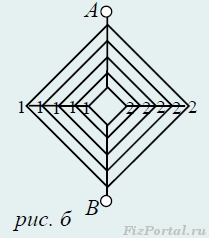
Если посмотрим на каркас слева, то получим изображение цепи в перспективе, приведенное на рисунке б.
Из симметрии этого рисунка видно, что потенциалы точек, обозначенных цифрой 1, одинаковы и равны потенциалам точек, обозначенных цифрой 2.
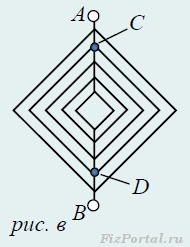
Исключим из рассмотрения пассивные резисторы, соединяющие точки 1 и 2 (рис. в).
Между точками С и D (рис. в) находится фигура, эквивалентное сопротивление которой равно искомому, т.к. цепь бесконечна.
Обозначим искомое сопротивление через Rх (рис. г)
и получим (аналогично решению задачи 1)
Второй корень уравнения отрицательный и не имеет смысла. Окончательный результат:
1.9. Преобразование и расчет цепей с помощью перехода «звезда» − «треугольник»
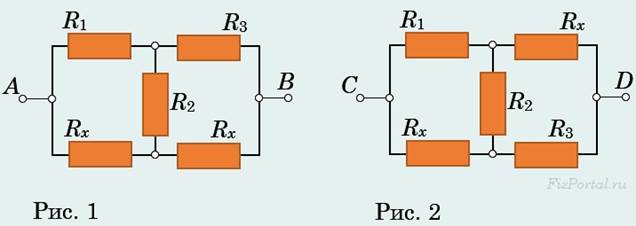
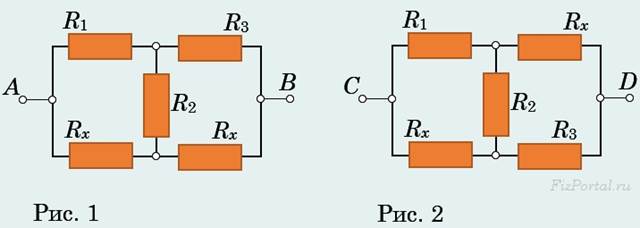
Задача 1: В электрических цепях (рис. 1 и 2) сопротивление RAB между зажимами A и B и сопротивление RCD между зажимами C и D равны, а сопротивления резисторов R1, R2 и R3 − заданы. Найдите все возможные значения сопротивления Rx.
Вначале немного теории:
Рассматриваемый метод основан на том, что сложную схему, имеющую три вывода (узла), можно заменить другой, с тем же числом выводов (узлов). Замену следует произвести так, чтобы сопротивление участка между двумя любыми выводами новой схемы было таким же, как у прежней. В результате получится цепь, сопротивление которой эквивалентно сопротивлению данной по условию. Общее сопротивление обеих цепей будет одинаковым. Однако, поскольку в результате такого преобразования изменяются токи внутри цепи, такую замену можно проводить только в тех случаях, когда не надо находить распределение токов.
Подобные преобразования широко известны для случая двух выводов. Так, например, два резистора сопротивлениями R1 и R2, включенные последовательно (Рис. 1), можно заменить одним резистором сопротивлением
Если резисторы включены параллельно (Рис. 2), то их можно заменить одним резистором сопротивлением
И в этих случаях распределение токов в цепи (или в части цепи) претерпевает изменения.
Рассмотрим более сложное преобразование схем, имеющих три вывода (трехполюсников). Иначе это называется преобразованием «звезды» (Рис. 3) в «треугольник» (Рис. 4), и наоборот.
Сопротивления резисторов в схеме «звезда» обозначаются с индексом точки, с которой соединен этот резистор, например, резистор r1 соединен с точкой 1. В «треугольнике» индексы резисторов соответствуют точкам, между которыми они включены, например, резистор R13 подключен к точкам 1 и 3.
Как отмечено выше, чтобы заменить одну из этих схем другой, нужно получить такие соотношения между их сопротивлениями, чтобы эквивалентные сопротивления между любыми точками были одинаковы для обеих схем (при условии сохранения числа этих точек).
Так, в «звезде» сопротивление между точками 1 и 2 равно r1 + r2, в «треугольнике»
Следовательно, для того чтобы сопротивления между точками 1 и 2 были одинаковы для обеих схем, необходимо, чтобы выполнялось следующее равенство:
Аналогично для точек 2 и 3 и для точек 1 и 3.
Сложим все эти уравнения и, поделив обе части на 2, получим:
Вычитая из этого уравнения поочередно предыдущие, получим:
Эти выражения легко запомнить:
знаменатель в каждой формуле есть сумма сопротивлений всех резисторов «треугольника», а в числителе дважды повторяется индекс, стоящий слева:
Аналогично получают и формулы обратного преобразования:
Последние выражения также легко запомнить и проверить: числитель у всех уравнений один и тот же, а в знаменателе стоит сопротивление резистора с индексом, которого не достает в левой части выражения.
Этот метод представляет собой наиболее универсальный подход к решению практически всех типов задач на разветвленные цепи.
А теперь приступим к решению задачи:
Наиболее просто сопротивления RAB и RCD можно вычислить, если соединение «треугольником» резисторов R1, R2 и Rx (на рисунках 5 и 6 оно обведено пунктирным контуром) заменить эквивалентным соединением «звездой» (рис. 7 и 8).
На данном этапе мы воздержимся от пересчета «треугольника» в «звезду», а будем считать, что rA, r1 и r2 нами уже найдены. Поскольку RAB = RCD, то и RMB = RND, так как rA соединено последовательно с каждым из них:
Так как в последнем уравнении знаменатели равны, то должны быть равны и числители:
После раскрытия скобок и приведения подобных членов это уравнение примет вид
Такое равенство возможно в двух случаях:
1. Rx = R3 − это один корень уравнения;
Данное равенство указывает на симметрию соединения «звездой», но симметрия «звезды» возможна только тогда, когда и исходная схема соединения «треугольником» обладает подобной симметрией, то есть когда R1= Rx − это второй корень уравнения. Других решений у составленного нами уравнения нет. Следовательно, возможны только два значения Rx:
При внимательном анализе схем (рис. 1 и 2) оба решения легко «угадываются», но их единственность не очевидна.
Для закрепления понимания метода решите следующую задачу:
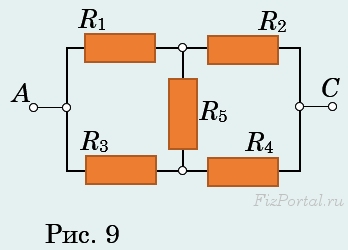
Задача 2: В схеме неуравновешенного моста (рис. 9) определите общее сопротивление цепи между точками А и С, если R1 = 1 Ом, R2 = 1,6 Ом, R3 = 2 Ом, R4 = 1,2 Ом, R5 = 2 Ом.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: 


Источник