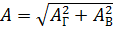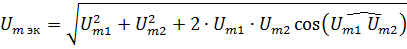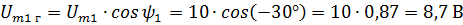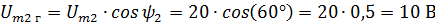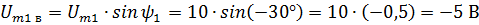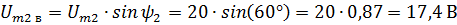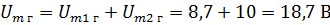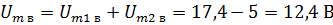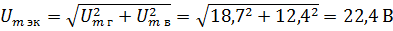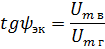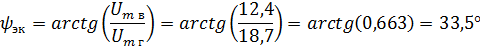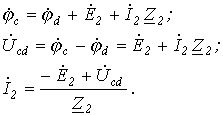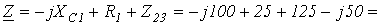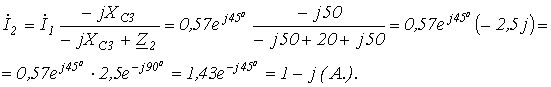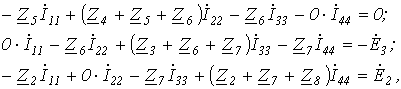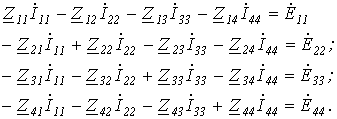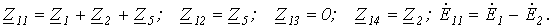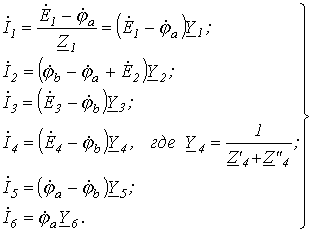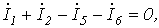Символический метод расчета цепей переменного тока

При таком подходе в общем случае получаются две результирующие составляющие — горизонтальная и вертикальная, которые всегда находятся друг к другу под одним и тем же углом, равным 90°.
По этим составляющим можно найти их равнодействующую, т. е. произвести их геометрическое сложение. Составляющие под прямым углом представляют катеты прямоугольного треугольника, а их геометрическая сумма — гипотенузу.
Можно также сказать, что геометрическая сумма численно равна диагонали параллелограмма, построенного на составляющих, как на его сторонах . Если горизонтальную составляющую обозначить АГ а вертикальную — АВ, то геометрическая сумма (1)
Находить геометрическую сумму прямоугольных треугольников гораздо легче, чем косоугольных. Легко видеть, что (2)
превращается в (1) если угол между составляющими составляет 90°. Поскольку cos 90 = 0, последний член в подкоренном выражении (2) исчезает, вследствие чего выражение резко упрощается. Обратим внимание на то, что перед словом «сумма» обязательно следует добавлять одно из трех слов: «арифметическая», «алгебраическая», «геометрическая».
Слово «сумма» без указания, какая именно, приводит к неопределенности, а в ряде случаев и к грубым ошибкам.
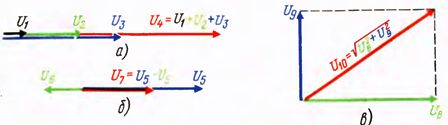
Напомним, что результирующий вектор равен арифметической сумме векторов в том случае, когда все векторы идут по одной прямой (или параллельно друг другу) в одинаковом направлении. При этом все векторы имеют знак плюс (рис. 1, а).
Если векторы идут по одной прямой, но направлены в противоположные стороны, то их равнодействующая равна алгебраической сумме векторов, в этом случае одни члены имеют знак плюс, а другие минус.
Например, в схеме рис. 1, б U6 = U4 — U5. Можно также сказать, что арифметическую сумму используют в тех случаях, когда угол между векторами равен нулю, алгебраическую, когда углы составляют 0 и 180°. Во всех остальных случаях сложение производят векторно, т. е. определяют геометрическую сумму (рис. 1, в).
Пример . Определить параметры эквивалентной синусоиды для цепи рис. 2, а символическим методом.
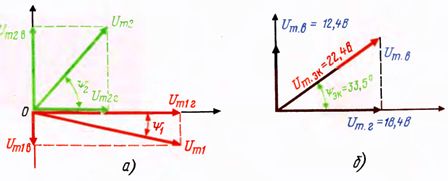
Решение. Нарисуем векторы Um1 Um2 и разложим их на составляющие. Из чертежа видно, что каждая горизонтальная составляющая представляет значение вектора, умноженное на косинус фазного угла, а вертикальная — значение вектора, умноженное на синус фазного угла. В данном случае
Очевидно, что общие горизонтальные и вертикальная составляющие равны алгебраическим суммам соответствующих составляющих. В данном случае
Получившиеся составляющие покажем на рис. 2, б. Определим значение Um для этого вычислим геометрическую сумму обеих составляющих:
Определим эквивалентный фазный угол ψэк. Из рис. 2,б видно, что отношение вертикальной составляющей к горизонтальной представляет тангенс эквивалентного фазного угла.
Таким образом, результирующая синусоида имеет амплитуду 22,4 В, начальную фазу 33,5° с таким же периодом, который имели составляющие. Заметим, что складывать можно только синусоиды с одинаковыми частотами поскольку при сложении синусоидальных кривых с различными частотами, результирующая кривая перестает быть синусоидальной и все понятия, приложимые только к гармоническим сигналам, становятся в этом случае неправомерными.
Проследим еще раз всю цепочку преобразований, которые приходится проделывать с математическими описаниями сигналов гармонической формы при выполнении различных расчетов.
Сначала временные функции заменяют векторными изображениями, затем каждый вектор раскладывают на две взаимно перпендикулярные составляющие, после чего просчитывают отдельно горизонтальные и вертикальные составляющие и, наконец, определяют значения результирующего вектора и его начальной фазы.
Такой путь расчета избавляет от необходимости графически складывать (а в ряде случаев делать и более сложные операции, например, перемножать делить, извлекать корни и т. д.) синусоидальные кривые и прибегать к расчетам с помощью формул косоугольных треугольников.
Однако рассчитывать отдельно горизонтальные и вертикальные составляющие операции достаточно громоздкие. При подобных расчетах очень удобным является такой математический аппарат, с помощью которого можно просчитать сразу обе составляющие.
Уже в конце прошлого века был разработан метод, позволяющий одновременно производить расчеты над числами, отложенными на взаимно перпендикулярных осях. Числа, откладываемые по горизонтальной оси, назвали вещественными, а по вертикальной оси — мнимыми. При расчетах этих чисел к вещественным добавляют множитель ± 1, а к мнимым — ±j (читается «жи»). Числа, состоящие из вещественной и мнимой частей, назвали комплексными, а метод расчетов, выполняемых с их помощью — символическим .
Поясним термин «символический». Те функции, которые подлежат расчету (в данном случае гармонические), являются оригиналами, а те выражения, которыми заменяют оригиналы — изображениями или символами.
При использовании символического метода все расчеты производят не над самими оригиналами, а над их символами (изображениями), которые в нашем случае представляют соответствующие комплексные числа, поскольку производить операции над изображениями значительно легче, чем над самими оригиналами.
По окончании всех операций над изображениями по результирующему изображению записывают оригинал, соответствующий получившемуся изображению. Символическим методом производят подавляющее большинство расчетов в электрических цепях.
Телеграмм канал для тех, кто каждый день хочет узнавать новое и интересное: Школа для электрика
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Не пропустите обновления, подпишитесь на наши соцсети:
Источник
Основы символического метода расчета. Методы контурных токов и узловых потенциалов.
Закон Ома для участка цепи с источником ЭДС
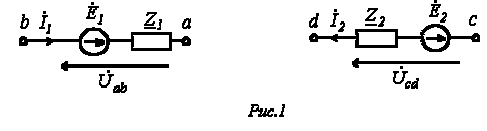 |
Возьмем два участка цепи a — b и c — d (см. рис. 1) и составим для них уравнения в комплексной форме с учетом указанных на рис. 1 положительных направлений напряжений и токов.
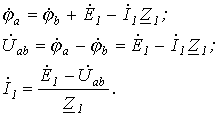
Объединяя оба случая, получим
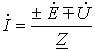 | (1) |
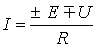 . . | (2) |
Формулы (1) и (2) являются аналитическим выражением закона Ома для участка цепи с источником ЭДС , согласно которому ток на участке цепи с источником ЭДС равен алгебраической сумме напряжения на зажимах участка цепи и ЭДС, деленной на сопротивление участка. В случае переменного тока все указанные величины суть комплексы. При этом ЭДС и напряжение берут со знаком “+”, если их направление совпадает с выбранным направлением тока, и со знаком “-”, если их направление противоположно направлению тока.
Основы символического метода расчета цепей
синусоидального тока
Расчет цепей переменного синусоидального тока может производиться не только путем построения векторных диаграмм, но и аналитически – путем операций с комплексами, символически изображающими синусоидальные ЭДС, напряжения и токи. Достоинством векторных диаграмм является их наглядность, недостатком – малая точность графических построений. Применение символического метода позволяет производить расчеты цепей с большой степенью точности.
Символический метод расчета цепей синусоидального тока основан на законах Кирхгофа и законе Ома в комплексной форме.
Уравнения, выражающие законы Кирхгофа в комплексной форме, имеют совершенно такой же вид, как и соответствующие уравнения для цепей постоянного тока. Только токи, ЭДС, напряжения и сопротивления входят в уравнение в виде комплексных величин.
1. Первый закон Кирхгофа в комплексной форме:
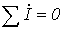 . . | (3) |
2. Второй закон Кирхгофа в комплексной форме:
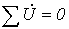 | (4) |
или применительно к схемам замещения с источниками ЭДС
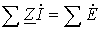 . . | (5) |
3. Соответственно матричная запись законов Кирхгофа в комплексной форме имеет вид:
. 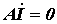 ; ; | (6) |
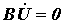 . . | (7) |
 | 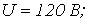 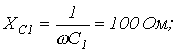 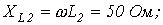 | |||
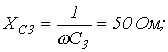 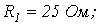 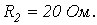 | ||||
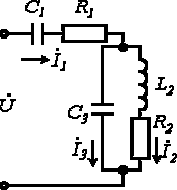
| Определить: | 1) полное комплексное сопротивление цепи 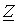 ; ; | |||
2) токи 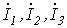 | ||||
| Рис. 2 | ||||
1. 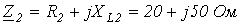
2. 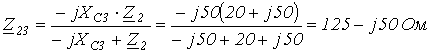
3.
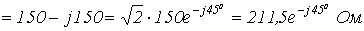
4. Принимая начальную фазу напряжения за нуль, запишем:
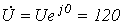
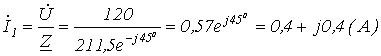
5. Поскольку ток распределяется обратно пропорционально сопротивлению ветвей (это вытекает из закона Ома), то
6. 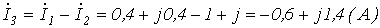
7. Аналогичный результат можно получить, составив для данной схемы уравнения по законам Кирхгофа в комплексной форме
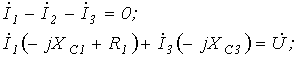 |
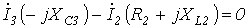 |
или после подстановки численных значений параметров схемы
Специальные методы расчета
Режим работы любой цепи полностью характеризуется уравнениями, составленными на основании законов Кирхгофа. При этом необходимо составить и решить систему с n неизвестными, что может оказаться весьма трудоемкой задачей при большом числе n ветвей схемы. Однако, число уравнений, подлежащих решению, может быть сокращено, если воспользоваться специальными методами расчета , к которым относятся методы контурных токов и узловых потенциалов.
Идея метода контурных токов: уравнения составляются только по второму закону Кирхгофа, но не для действительных, а для воображаемых токов, циркулирующих по замкнутым контурам, т.е. в случае выбора главных контуров равных токам ветвей связи. Число уравнений равно числу независимых контуров, т.е. числу ветвей связи графа 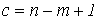
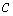
Направления истинных и контурных токов выбираются произвольно. Выбор положительных направлений перед началом расчета может не определять действительные направления токов в цепи. Если в результате расчета какой-либо из токов, как и при использовании уравнений по законам Кирхгофа, получится со знаком “-”, это означает, что его истинное направление противоположно.
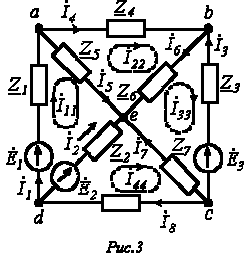
Пусть имеем схему по рис. 3.
Выразим токи ветвей через контурные токи:
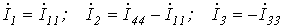
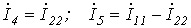
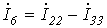
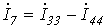
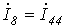
Обойдя контур aeda, по второму закону Кирхгофа имеем
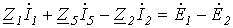
Поскольку 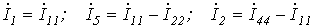
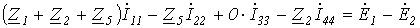
Таким образом, получили уравнение для первого контура относительно контурных токов. Аналогично можно составить уравнения для второго, третьего и четвертого контуров:
совместно с первым решить их относительно контурных токов и затем по уравнениям, связывающим контурные токи и токи ветвей, найти последние.
Однако данная система уравнений может быть составлена формальным путем:
При составлении уравнений необходимо помнить следующее:
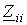
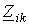
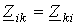
члены на главной диагонали всегда пишутся со знаком “+”;
знак “+” перед остальными членами ставится в случае, если через общее сопротивление 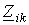
если i- й и k- й контуры не имеют общих сопротивлений, то 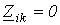
в правой части уравнений записывается алгебраическая сумма ЭДС, входящих в контур: со знаком “+”, если направление ЭДС совпадает с выбранным направлением контурного тока, и “-”, если не совпадает.
В нашем случае, для первого уравнения системы, имеем:
Следует обратить внимание на то, что, поскольку 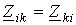
Если в цепи содержатся помимо источников ЭДС источники тока, то они учитываются в левых частях уравнений как известные контурные токи: k- й контурный ток, проходящий через ветвь с k- м источником тока равен этому току 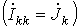
Метод узловых потенциалов
Данный метод вытекает из первого закона Кирхгофа. В качестве неизвестных принимаются потенциалы узлов, по найденным значениям которых с помощью закона Ома для участка цепи с источником ЭДС затем находят токи в ветвях. Поскольку потенциал – величина относительная, потенциал одного из узлов (любого) принимается равным нулю. Таким образом, число неизвестных потенциалов, а следовательно, и число уравнений равно 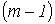
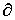
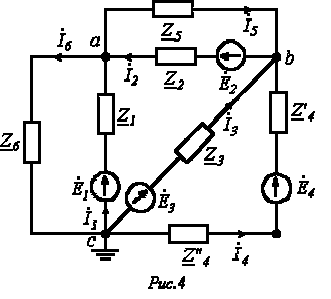
Пусть имеем схему по рис. 4, в которой примем 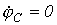
Допустим, что 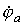
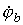
Запишем уравнение по первому закону Кирхгофа для узла а :
и подставим значения входящих в него токов, определенных выше:
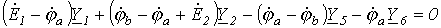
Сгруппировав соответствующие члены, получим:
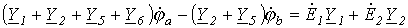
Аналогично можно записать для узла b :
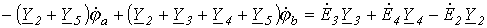
Как и по методу контурных токов, система уравнений по методу узловых потенциалов может быть составлена формальным путем. При этом необходимо руководствоваться следующими правилами:
1. В левой части i- го уравнения записывается со знаком “+”потенциал 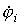
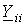
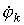
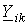
Из сказанного следует, что все члены 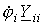
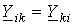
2. В правой части i- го уравнения записывается так называемый узловой ток 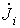
В заключение отметим, что выбор того или иного из рассмотренных методов определяется тем, что следует найти, а также тем, какой из них обеспечивает меньший порядок системы уравнений. При расчете токов при одинаковом числе уравнений предпочтительнее использовать метод контурных токов, так как он не требует дополнительных вычислений с использованием закона Ома. Метод узловых потенциалов очень удобен при расчетах многофазных цепей, но не удобен при расчете цепей со взаимной индуктивностью.
1. Основы теории цепей: Учеб.для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
1. В ветви на рис. 1 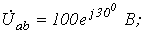
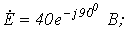
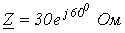
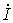
Ответ: 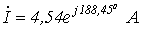
2. В чем заключается сущность символического метода расчета цепей синусоидального тока?
3. В чем состоит сущность метода контурных токов?
4. В чем состоит сущность метода узловых потенциалов?
5. В цепи на рис. 5 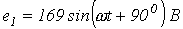
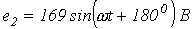
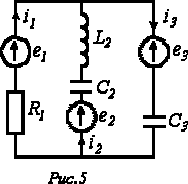
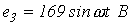
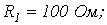
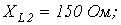
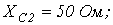
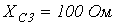
Ответ: 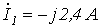
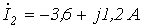
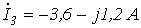
6. В цепи на рис. 6 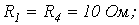
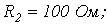
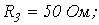
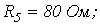
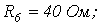
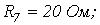
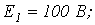
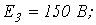
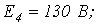
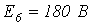
Ответ: 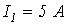
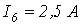
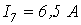
Источник