Покрытие графа непересекающимися по ребрам цепями
Количество таких цепей равно k /2, где k – количество вершин с нечетными степенями, оно всегда четно.
Если k = 2, то получается эйлерова цепь.
Если граф не удовлетворяет условиям Эйлера, то для нахождения покрытия графа непересекающимися по ребрам цепями надо дополнить граф до эйлерова графа, построить эйлеров цикл, а затем удалить введенные ребра (и вершины). Если граф эйлеров, то просто строим эйлеров цикл или эйлерову цепь.
Для преобразования графа в эйлеров граф можно:
1) продублировать все ребра (дуги) графа, или
2) добавить фиктивную вершину и соединить ее ребрами с вершинами, имеющими нечетную степень; таких вершин четное число, поэтому степень введеной вершины будет четной и, следовательно, все вершины будут удовлетворять условиям Эйлера, или
3) разбить множество вершин с нечетными степенями на пары и соединить вершины каждой пары ребром или маршрутом кратчайшей длины.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Источник
4. Покрытие графа непересекающимися по ребрам цепями
Количество таких цепей равно k/2, где k – количество вершин с нечетными степенями, оно всегда четно.
Если k = 2 , то получается эйлерова цепь.
Если граф не удовлетворяет условиям Эйлера, то для нахождения покрытия графа непересекающимися по ребрам цепями надо дополнить граф до эйлерова графа, построить эйлеров цикл, а затем удалить введенные ребра (и вершины). Если граф эйлеров, то просто строим эйлеров цикл или эйлерову цепь.
Для преобразования графа в эйлеров граф можно
– продублировать все ребра (дуги) графа, или
– добавить фиктивную вершину и соединить ее ребрами с вершинами, имеющими нечетную степень; таких вершин четное число, поэтому степень введеной вершины будет четной и, следовательно, все вершины будут удовлетворять условиям Эйлера, или
– разбить множество вершин с нечетными степенями на пары и соединить вершины каждой пары ребром или маршрутом кратчайшей длины.
Пример. Пусть задан графG(8,13), показанный на рис. 20.8.
Требуется покрыть граф непересекающимися по ребрам цепями.
Введем фиктивную вершину 9 и соединим ее фиктивными ребрами с вершинами 1, 2, 5, 8, имеющими нечетные степени (см. рис. 20.9).
Пусть vнач= 9,i= 1,j= 1 (i– формирователь индексов ребер основных циклов,j– формирователь индексов ребер частных циклов, возникающих при построении очередного основного цикла).
Случайно выбирая в каждой попавшейся в маршруте вершине очередное ребро (среди ребер, не имеющих индекса), строим первый основной цикл с началом в вершине 9. Пусть это будет цикл 9p2b3g6j8t9. При строительстве этого цикла частных циклов не образовалось.
Р
исунок 20.8
Ребрам построенного основного цикла присвоим индексы, равные значению i= 1 (см. рис. 20.10).
Р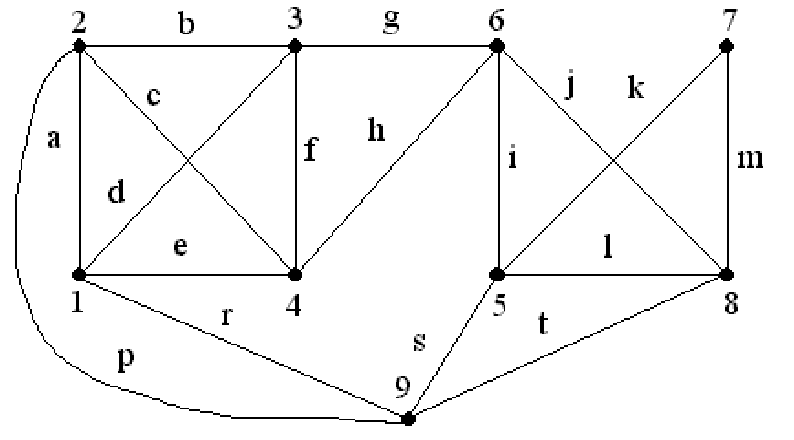
исунок 20.9
Р
исунок 20.10
Выбираем вершину, принадлежащую построенному циклу и имеющую ребра без индексов. Пусть это будет опять вершина 9.
Полагаем i=i+j= 1 + 1 = 2,j= 1.Строим второй основной цикл с началом в вершине 9.
Пусть построили такой маршрут 9r1a2c4f3d1. Замечаем, что при вершине 1 образовался частный цикл 1a2c4f3d1. Ребрам этого цикла присвоим индексi+j= 2 + 1 = 3 и исключаем их из основного цикла. Переменнойjприсваиваем новое значениеj=j+ 1 =1 + 1 = 2.
Продолжаем строить основной цикл от вершины 1 – 9r1e4h6i5k7m8l5 – замечаем, что образовался второй частный цикл при вершине 5 – 5k7m8l5. Его ребрам присвоим индексi+j= 2 + 2 = 4 и исключаем их из основного цикла, переменнойjприсвоим новое значениеj=j+ 1 = 2 + 1 =3.
Продолжаем строить основной цикл от вершины 5. Получаем 9r1e4h6i5s9. Частных циклов больше не образовалось.
Ребрам полученного основного цикла присвоим индекс, равный i= 2. Все ребра графа имеют индексы. Первая фаза закончена (см. рис. 20.11).
Р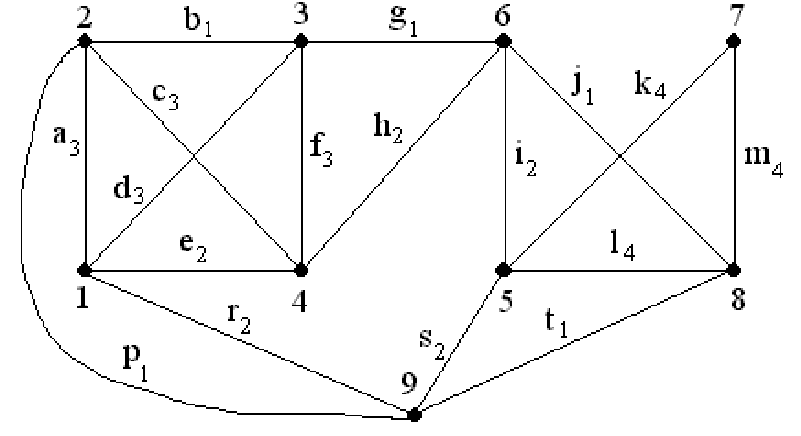
исунок 20.11
1. Строим эйлеров цикл с началом в вершине 9:
2. Удалим введенную вершину 9 и инцидентные ей ребра. Получим две покрывающие граф цепи, не имеющие общих ребер
Источник
Непересекающиеся цепи и разделяющие множества
Пусть G (V, Е) — связный граф, и и v — две его несмежные вершины. Две цепи (и, v) называются вершинно-непересекающимися, если у них нет общих вершин, отличных от и и v.
Две цепи 
называются рёберно-непересекающимися, если у них нет общих рёбер.
Замечание 1. Если две цепи вершинно не пересекаются, то они и рёберно не пересекаются.
Обозначим через Р (и, v) множество вершинно-непересекающихся цепей .
Множество R вершин (и/или рёбер) графа G разделяет две вершины и и v, если и и v принадлежат разным компонентам связности графа G-R.
Разделяющее множество рёбер называется разрезом. Разделяющее множество вершин для вершин и и v обозначим R (u, v).
Для заданных вершин и и v множества Р (и, v) и S (u, v) можно выбирать различным образом.
Из определений следует, что любое множество P (u,v) вершинно-непересека- ющихся цепей обладает тем свойством, что
,
а любое разделяющее множество вершин R(u, v) обладает тем свойством, что
& 
& 
.
Замечание 2. Если и и v принадлежат разным компонентам связности графа G, то \Р (и, v)| = 0 и \R (и, v)| = 0.
Пример 11.1. В графе, диаграмма которого представлена на рис. 32, можно выбрать множества вершинно-непересекающихся путей Р 1 = <(и, a, d, v), (u, b, e, v)>и Р 2 =<(u, b, d, v), (u, c, e, v)>. Заметим, что путь (u, c, b, d, v) образует множество Р 3 вершинно-непересекающихся путей, состоящее из одного элемента. Множества вершин R 1 =< a, b, c > и R 2 =< d, e > являются разделяющими для вершин u и v.
Рис. 32. Вершинно-непересекающиеся пути и разделяющие множества вершин
Теорема Менгера в «вершинной форме»
Теорема (Менгера, 1927 г.). Пусть u и v — несмежные вершины в графе G. Наименьшее число вершин в множестве, разделяющем и и v, равно наибольшему числу вершинно- непересекающихся простых -цепей:
Замечание 3. Легко видеть, что 
. Действительно, любая -цепь проходит через R. Если бы 
, то в R была бы вершина, принадлежащая более чем одной цепи из Р, что противоречит выбору Р. Таким образом, для 
и 
. Следовательно, 
. Утверждение теоремы состоит в том, что в любом графе существуют такие Р и R, что достигается равенство | Р | = | R |.
Доказательство. Пусть G — связный граф, и и v — несмежные вершины. Совместная индукция по р и q. База: наименьший граф, удовлетворяющий условиям теоремы, состоит из трех вершин u,w,v и двух рёбер (u,w) и(w,v). В нём P(u,v) = < 
> и R(u,v) = < w >. Таким образом, | Р (u,v)| = | R (u,v)| = 1. Пусть утверждение теоремы верно для всех графов с числом вершин меньше р и/или числом рёбер меньше q. Рассмотрим граф G с р вершинами и q ребрами. Пусть u,v 
V, причём u,v — не смежны и R — некоторое наименьшее множество вершин, разделяющее и и v. Обозначим п: = 
Рассмотрим три случая.
[ 1 ] Пусть в R есть вершины, несмежные сu и несмежные с v. Тогда граф G-R состоит из двух нетривиальных графов G 1 и G 2. Образуем два новых графа Gu и Gv, стягивая нетривиальные графы G 1 и G 2 к вершинам и и v соответственно: Gu: = G/G 1, Gv: = G/G 2 (рис. 33).
R по-прежнему является наименьшим разделяющим множеством для u и v как в Gu, так и в Gv. Так как G 1 и G 2 нетривиальны, то Gu и Gv имеют меньше вершин и/или рёбер, чем G. Следовательно, по индукционному предположению в Gu и в Gv имеется п вершинно-непересекающихся простых цепей. Комбинируя отрезки этих цепей от и до R и от R до v, получаем п вершинно-непересекающихся простых цепей в G.
[ 2 ] Пусть все вершины R смежны с и или с v (для определённости пусть с и) и среди вершин S есть вершина w, смежная одновременно с и и с v (рис. 34).
Рассмотрим граф G’: = G — w. В нем R — w — разделяющее множество для и и v, причём наименьшее. По индукционному предположению в G’ имеется | R-w | = n — 1 вершинно-непересекающихся простых цепей. Добавим к ним цепь 
. Она простая и вершинно не пересекается с остальными. Таким образом, имеем п вершинно-непересекающихся простых цепей в G.t
Рис. 33. К доказательству теоремы Менгера, случай 1
Рис. 34. К доказательству теоремы Менгера, случай 2
[ 3 ] Пусть теперь все вершины R смежны с и или с v (для определённости пусть с u) и среди вершин R нет вершин, смежных одновременно с вершиной u ис вершиной v. Рассмотрим кратчайшую 
-цепь 
, 
(рис. 35).
Рис. 35. К доказательству теоремы Менгера, случай 3
Рассмотрим граф G’: = G/ < w 1, w 2>, полученный из G склейкой вершин w 1и w 2в вершину w 1. Имеем 
, в противном случае цепь была бы ещё более короткой. Следовательно, в графе G’ множество R по-прежнему является наименьшим, разделяющим и и v, и граф G’ имеет по крайней мере на одно ребро меньше. По индукционному предположению в G’ существуют п вершинно- непересекающихся простых цепей. Но цепи, которые не пересекаются в G’, не пересекаются и в G. Таким образом, получаем п вершинно-непересекающихся простых цепей в G. Что и требовалось доказать.
Варианты теоремы Менгера
Теорема Менгера представляет собой весьма общий факт, который в разных формулировках встречается в различных областях математики. Комбинируя верши- но- и рёберно-непересекающиеся цепи, разделяя не отдельные вершины, а множества вершин, используя инварианты 
и 
, можно сформулировать и другие утверждения, подобные теореме Менгера. Например:
Теорема. Для любых двух несмежных вершин и и v графа G наибольшее число рёберно-непересекающихся -цепей равно наименьшему числу рёбер в (и, v) -разрезе.
Теорема. Чтобы граф G был п-связным, необходимо и достаточно, чтобы любые две несмежные вершины были соединены не менее чем п вершинно-непересекающи- мися простыми цепями.
Другими словами, в любом графе G любые две несмежные вершины соединены не менее чем (G) вершинно-непересекающимися простыми цепями.
Так же можно отметить и связь между теоремами Менгера и Форда и Фалкерсона.
Источник