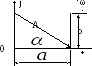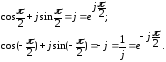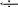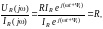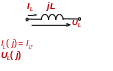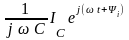Комплексный метод расчета электрических цепей
Существенное упрощение достигается изображением синусоидальных функций времени комплексными числами.
Существует несколько форм представления комплексного числа:
— алгебраическая форма: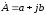 
;
— показательная (или экспоненциальная) форма: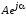 
;
— тригонометрическая форма: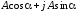 
.
Все эти формы связаны между собой, в частности, модуль числа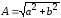 
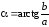
, аргумент
.
Для геометрического изображения используют прямоугольную систему координат, в которой по горизонтальной оси откладываются вещественные числа, а по вертикальной – мнимые:
; 
; 
.
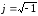
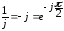
Для вещественной и мнимой частей комплексного числа употребляют также обозначения: 
,
.
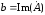
Две комплексные величины, имеющие равные модули и равные, но противоположные по знаку аргументы, называют сопряженными.
Если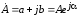 
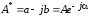
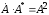
, то сопряженное ему комплексное число запишется в форме
. При этом соблюдается равенство:
.
Полезно помнить, что 
Пусть имеем синусоидально изменяющийся ток с начальной фазой φi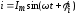 
.
Его можно представить в форме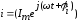 
.
Таким образом, синусоидальный ток рассматривают как комплексное изображение синусоидального тока, которое при заданной частоте ω определяется двумя величинами – амплитудой и начальной фазой:
.
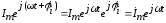
Здесь комплексное число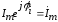 
называюткомплексной амплитудой тока.
Рассмотрим теперь выражение для производной по времени от синусоидального тока:
.
Изображение производной будет иметь вид:
.
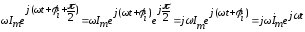
Таким образом, операция дифференцирования действительной функции заменяется умножением ее комплексного изображения на 
.
Рассмотрим изображение интеграла от синусоидальной функции
.
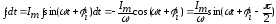
Искомое изображение интеграла будет иметь вид:
.
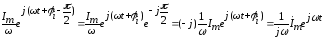
Следовательно, операция интегрирования действительной функции заменяется делением ее комплексного изображения на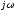 
.
Таким образом, комплексный метод позволяет заменить интегро-дифференциальное уравнение, содержащее функции времени, алгебраическим уравнением с их комплексными изображениями.
1. Замена заданных функций времени их комплексными изображениями.
2. Замена всех уравнений, составленных по закону Кирхгофа, алгебраическими уравнениями для комплексных изображений.
3. Нахождение комплексных изображений искомых функций.
4. Переход к оригиналам этих функций.
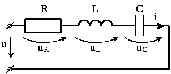
В качестве примера рассмотрим цепь с последовательно соединенными элементами R,L и C, к зажимам которой приложено напряжение, изменяющееся по синусоидальному закону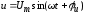 
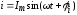
. Требуется найти ток в цепи:
.
1) Заменяем функции времени их изображениями: 
,
.
2) Составляем уравнение по второму закону Кирхгофа:
.
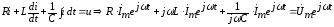
Полученное уравнение является алгебраическим. Все слагаемые имеют общий множитель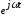 
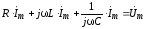
. Окончательно получаем уравнение в комплексных амплитудах:
.
3) Из последнего уравнения легко определяется комплексная амплитуда тока:
,
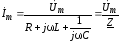
где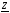 
– комплексное сопротивление цепи.
4) Зная выражение для комплексной амплитуды тока в виде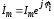 
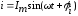
, можем, используя обратный переход, записать выражение для мгновенного тока:
.
Обычно рассматривают действующие значения токов и напряжений. Так как действующие синусоидальные токи и напряжения меньше их амплитуд в 
раз, то обычно вместо комплексных амплитуд рассматривают комплексные действующие величины:
,
.
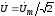
Источник
Установочная лекция 4 (2 ч.) комплексный метод анализа электрических цепей
4.1. Комплексный метод расчета цепей синусоидального тока.
4.2. Резонансные явления в цепях синусоидального тока.
4.3. Понятие «индуктивно связанные цепи».
4.1А. Комплексный метод расчета цепей синусоидального тока
Комплексный (называемый также символический) метода расчёта, применяют обычно для расчёта сложных электрических цепей синусоидального тока в установившихся режимах.
Порядок расчёта выходной синусоидальной функции f1(t) линейной электрической цепи с п ветвями комплексным методом представлен в табл. 4.1.
Пользуясь комплексным методом, определить выходную синусоидальную функцию f1(t) линейной цепи с n ветвями
Область синусоидальных функций
Область функций комплексного переменного j
Записывают посредством законов Кирхгофа для независимых узлов и контуров цепи систему из n алгебраических и интегрально-дифференциальных уравнений, в которую входит искомая функция f1(t)
Получают систему из n комплексных алгебраических уравнений, записанных по законам Кирхгофа для независимых узлов и контуров цепи
Широкое применение комплексного метода расчёта цепей синусоидального тока в установившихся режимах объясняется следующими соображениями:
метод предельно формализован, что упрощает расчёт электрических цепей синусоидального тока сложной конфигурации;
рассмотренные в лекции 2 методы расчёта цепей постоянного тока (ЗК, МУН, МКТ, МЭГ и др.) применимы к расчёту цепей синусоидального тока комплексным методом. По внешним признакам они очень схожи: сохраняются все правила составления систем уравнений, однако при их записи посредством комплексных чисел используют комплексные сопротивления Zk ветвей цепи (вместо сопротивлений Rk), а вместо синусоидальных электрических величин (ЭДС e, напряжения u, тока i) их комплексы: E, U, I;
посредством комплексного метода рассчитывают частотные зависимости (характеристики) электрических величин.
Пассивный элемент электрической цепи характеризуется своим комплексным сопротивлением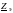 
= 
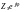
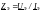
комплексным числом, равным отношению комплекса напряжения на зажимах данного элемента к комплексу тока этого элемента при t = 0, т.е.
.
Зная компонентные уравнения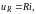 
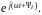
uC = 
пассивных элементов R, L и С электрической цепи, и операции дифференцирования и интегрирования комплексного тока I(j) = I 
путём несложных преобразований получают комплексы сопротивлений и компонентные уравнения пассивных элементов в комплексной форме (табл. 4.2).
Комплексное сопротивление и компонентное уравнение элемента
ZR = 
ZL = 
IС(j) = IС e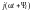 
,
UС (j) = 
ZС = 
Источник