Комплексное действующее значение тока цепи

Комплексные амплитуды, комплексные действующие значения, комплексы действующих значений

Комплексные амплитуды напряжения

при анализе установившегося синусоидального режима соответствуют сигналам синусоидальной формы напряжения

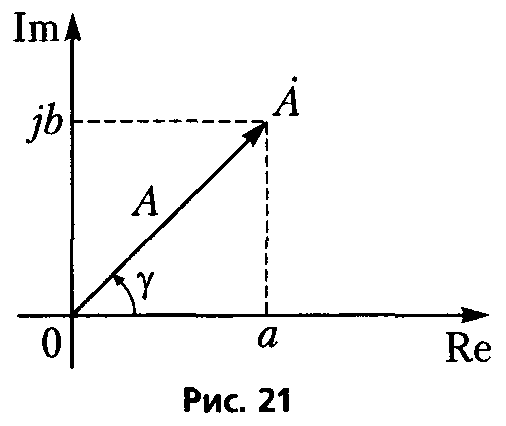
Комплексные амплитуды представляют векторами на комплексной плоскости, как комплексное число (рис. 21)

A ˙ = A e j γ = A cos γ + j A sin γ = a + j b ,

действительная часть комплексного числа

мнимая часть комплексного числа

j 2 = − 1, j ⋅ ( − j ) = − j 2 = − ( − 1 ) = 1, 1 j = j j 2 = j − 1 = − j .

Сопряженное комплексное число

A * = A e − j γ = A cos ( − γ ) + j A sin ( − γ ) = A cos γ − j A sin γ = a − j b ,

где положительный отсчет угла γ производят против часовой стрелки от «правого горизонта».

Комплексные амплитуды используют при обосновании метода комплексных амплитуд для расчета установившегося синусоидального режима

u ( t ) = Re U ˙ m e j ω t = Re U m e j α u e j ω t = Re U m e j ( ω t + α u ) = U m cos ( ω t + α u ) ; i ( t ) = Re I ˙ m e j ω t = Re I m e j α i e j ω t = Re I m e j ( ω t + α i ) = I m cos ( ω t + α i ) ,

где e j ω t — оператор вращения, U ˙ m e j ω t , I ˙ m e j ω t – вращающиеся векторы, поскольку их суммарная фаза γ = ωt + α равномерно увеличивается с увеличением времени t.

Комплексные действующие значения или комплексы действующих значений:

комплексное действующее напряжение или комплекс действующего напряжения

U ˙ = U e j α u = U ˙ m 2 = U m 2 e j α u ,

комплексный действующий ток или комплекс действующего тока

I ˙ = I e j α i = I ˙ m 2 = I m 2 e j α i .

комплексы действующих значений, комплексные действующие значения, Комплексные амплитуды

Источник

Расчет цепей переменного тока

Расчет электрических цепей переменного синусоидального тока производится в комплексной форме. При этом величины синусоидальных ЭДС и токов представляются в виде комплексных амплитуд или комплексных действующих значений, а все элементы в схеме – в виде комплексных сопротивлений.

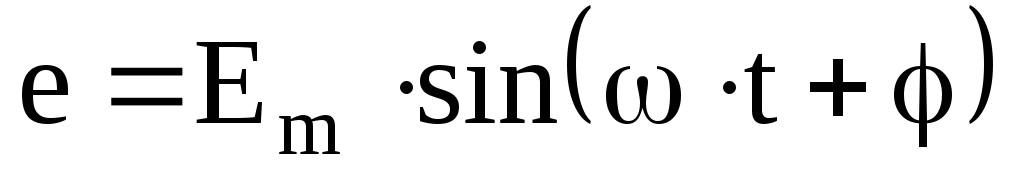
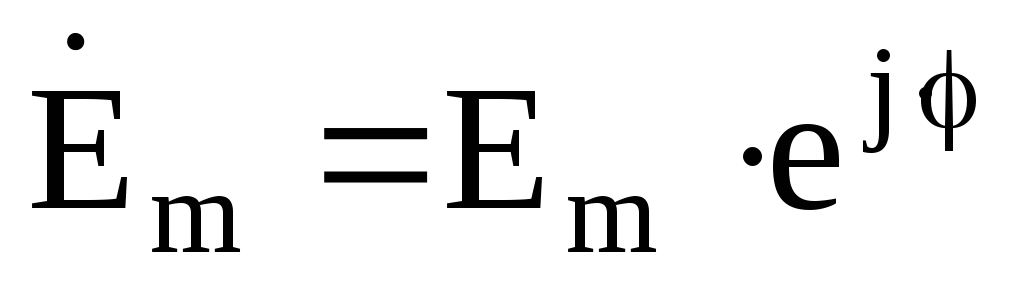
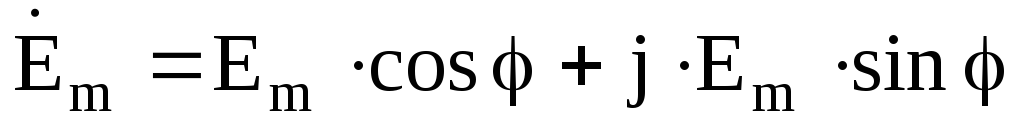
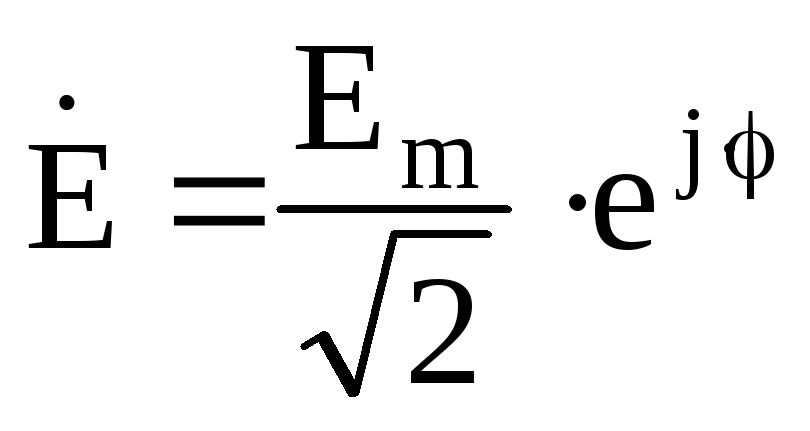
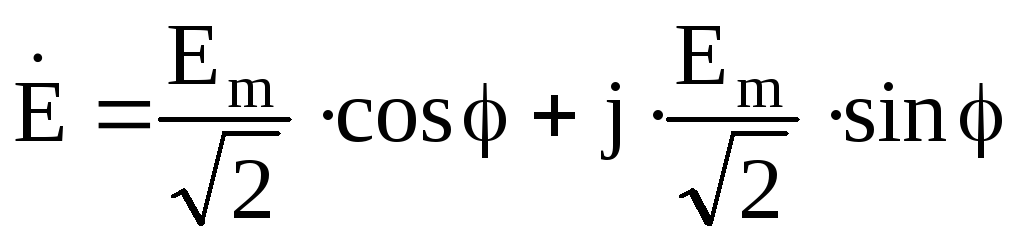
Например, если ЭДС источника равна , то комплексная амплитуда запишется в виде— в показательной форме записи, или— в алгебраической форме. Комплексное действующее значение синусоидальной ЭДС:— в показательной форме записи, или— в алгебраической форме.

Комплексные сопротивления элементов электрической цепи переменного тока:

— для идеального сопротивления,

— для идеальной индуктивности,

— для идеальной емкости.

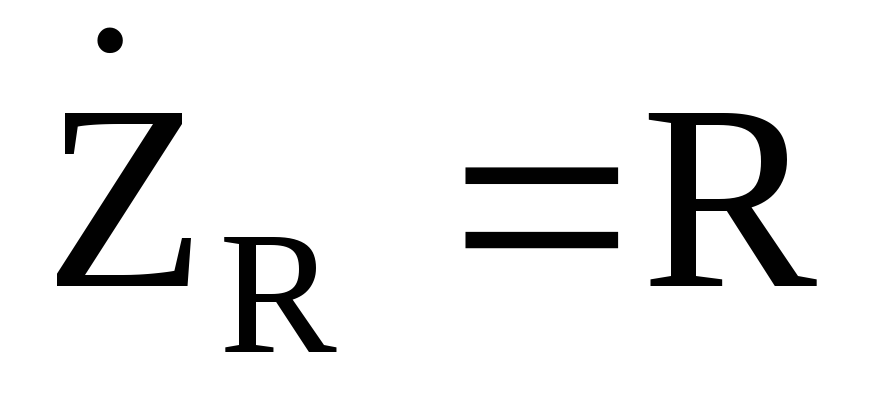
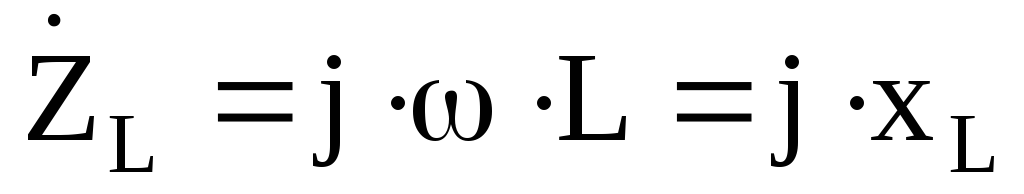
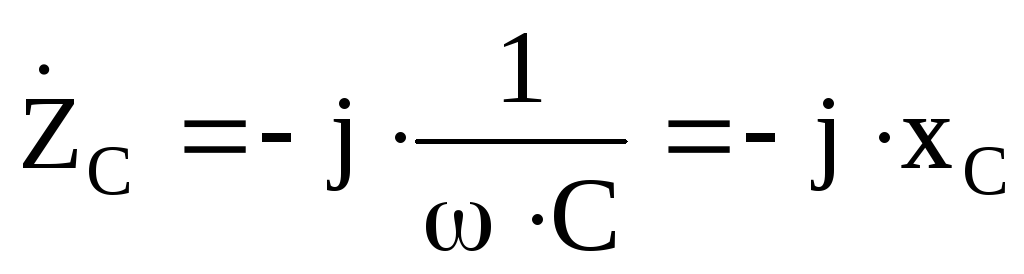
Далее расчет электрической цепи переменного тока можно вести любым методом, известным из раздела – «электрические цепи постоянного тока». При этом используется математический аппарат, разработанный для операций с комплексными числами.

Применяются три формы записи комплексного значения синусоидальной величины:

— показательная форма,

— алгебраическая форма,

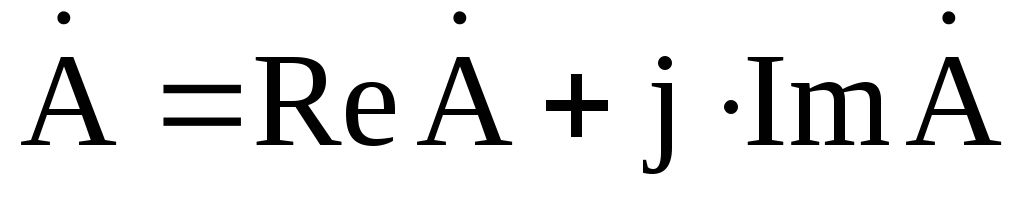
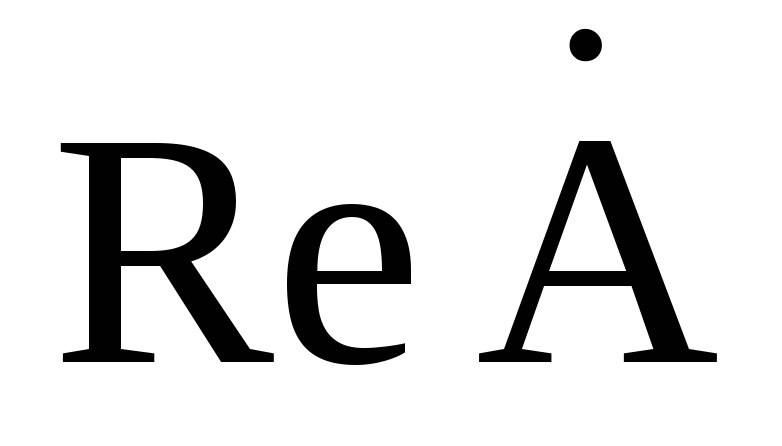
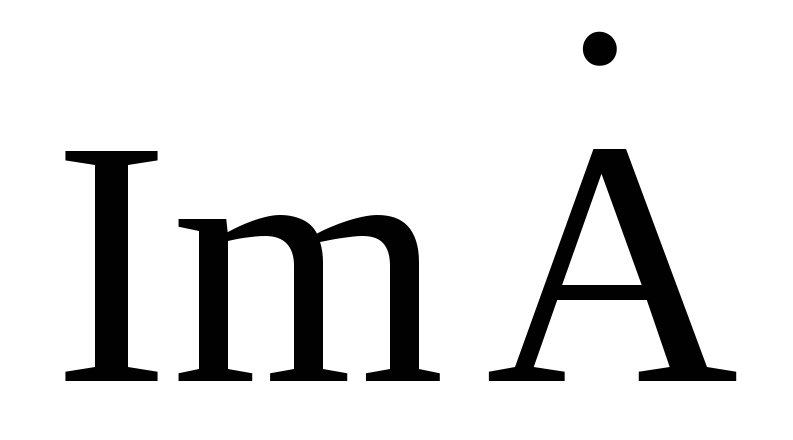
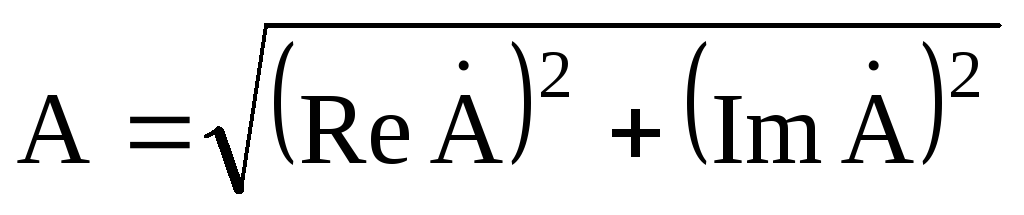
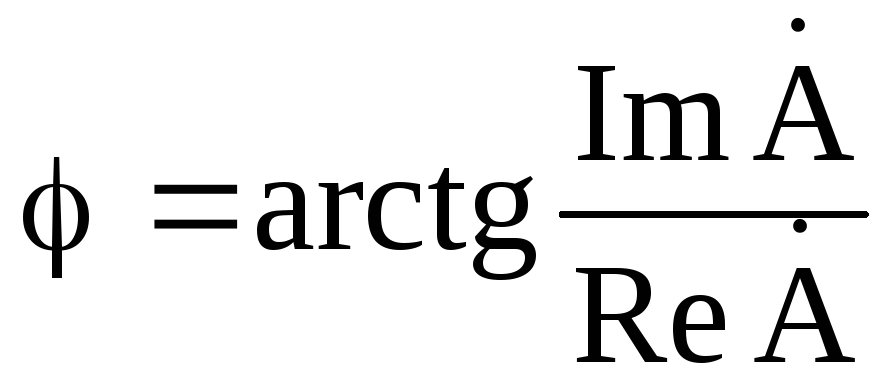
где и— действительная и мнимая часть комплексного значения синусоидальной величины. Переход от алгебраической формы к показательной осуществляется по формулам:

;.

Переход от показательной формы к тригонометрической осуществляется по формуле Эйлера:

.

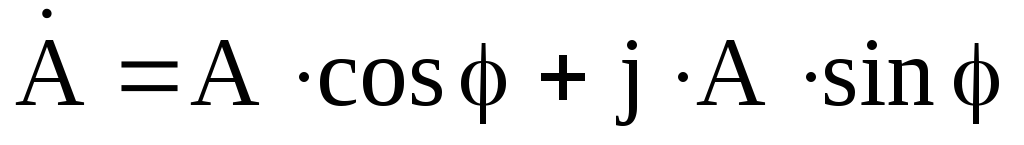
Сложение и вычитание комплексных величин производится в алгебраической форме, а умножение и деление в показательной.

При анализе цепей синусоидального тока применяют главным образом комплексные действующие значения синусоидальных величин, сокращенно их называют комплексными значениями.

Расчет однофазных цепей

Р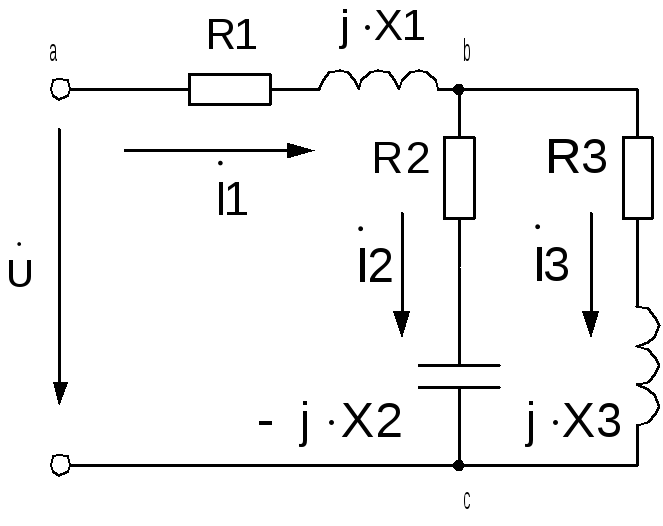асчет однофазных цепей переменного тока при наличии одного источника синусоидальной ЭДС производится методом эквивалентных преобразований. Рассмотрим пример расчета однофазной цепи приведенной на рис.

Рис. 2.4. Схема электрической цепи к примеру расчета

Пример расчета однофазной цепи

По заданным значениям активных и реактивных сопротивлений и напряжению источника определить токи во всех ветвях схемы и падения напряжения на ее участках. Определить комплекс полной мощности, активную и реактивную мощность. Расчет произвести комплексным методом. Выполнить проверку правильности расчета с использованием баланса активных мощностей схемы. Построить векторную диаграмму. Построить мгновенные значения синусоидальных токов ветвей. Исходные данные для расчета приведены в таблице.

Источник

3.5. Символический метод расчета цепей переменного тока

Для использования символического метода при расчете цепей переменного тока необходимо перейти от уравнений, составленных для мгновенных значений, которые являются дифференциальными, к алгебраическим. Этот переход осуществляется следующим образом.

В электрических цепях синусоидального тока для реактивных элементов L и C вводят понятие комплексных сопротивлений

(3. 22)

Здесь множитель j учитывает сдвиг фазы между током и напряжением в индуктивности и емкости. Значение активного сопротивления остается таким же, как в цепях постоянного тока.

Мгновенные значения токов в ветвях и напряжений на элементах заменяются их комплексными амплитудными (либо комплексными действующими) значениями. После замены ток и напряжения на элементах будут иметь вид

или ,

или ,

или ,

или , (3. 23)

или .

В дальнейшем, при выполнении расчетов, будем использовать комплексные действующие значения напряжений и токов.

Рассмотрим неразветвленную цепь переменного тока, содержащую источник ЭДС, активное сопротивление, емкость и индуктивность (рис. 3. 10).

При переходе от мгновенных значений токов и напряжений к комплексным (амплитудным) действующим оказывается возможным использование для расчета цепей переменного тока законов Ома и Кирхгофа, а также методов, применяемых для расчета электрических цепей постоянного тока (методы наложения, контурных токов, эквивалентного генератора и др.). Законы Ома и Кирхгофа для цепей переменного тока в символической форме имеют вид

, , . (3. 24)

Рис. 3. 10. Пример электрической цепи переменного тока

рименение символического метода расчета электрических цепей переменного тока позволяет перейти от решения дифференциальных уравнений к решению алгебраических уравнений, что значительно упрощает расчеты. Рассмотрим порядок расчета символическим методом электрической цепи переменного тока, показанной на рис. 3. 10. В цепи действует ЭДС

. (3. 25)

В этой цепи по второму закону Кирхгофа для мгновенных значений тока можно составить интегрально-дифференциальное уравнение вида

. (3. 26)

В символической форме это уравнение примет вид

. (3. 27)

Из последнего уравнения получим формулу для комплексного тока цепи

, (3. 28)

где – комплексное сопротивление цепи. В общем случае комплексное сопротивление имеет действительную R и мнимую X части:

. (3. 29)

Получив выражение для комплексного значения тока , далее перейдем к мгновенным значениям тока

. (3. 30)

Из-за комплексного характера полного сопротивления цепи между ЭДС и током возникает сдвиг фазы

. (3. 31)

Рассчитав ток , далее можно определить напряжения на пассивных элементах

, , . (3. 32)

Рис. 3. 11. Векторно-топографическая диаграмма для схемы на рис. 3. 10

о полученным данным строят векторную диаграмму токов, отображающую комплексные токи в цепи, и топографическую диаграмму напряжений, отображающую комплексные потенциалы в цепи (рис. 3. 11). Векторная диаграмма токов является интерпретацией I закона Кирхгофа, а топографическая диаграмма напряжений – интерпретацией II закона Кирхгофа для электрической цепи синусоидального тока в векторной форме. Векторную и топографическую диаграммы строят на одном графике в разных масштабах. Совместное построение диаграмм позволяет демонстрировать сдвиги фаз между токами и напряжениями в элементах электрической цепи.

Сначала строят векторную диаграмму токов. Для ее построения векторы всех токов, протекающих в цепи, откладывают из начала координат. В процессе построения графическим методом контролируют соблюдение первого закона Кирхгофа. В схеме рис. 3. 10 протекает только один ток величиной I и фазой .

Для построения топографической диаграммы напряжений на схеме электрической цепи расставляют точки с различающимися потенциалами и нумеруют их начиная с 0. За 0-ю точку обычно принимают отрицательный электрод источника ЭДС. Точка 0 совпадает с началом координат на комплексной плоскости. Потенциалы расставляют, двигаясь против направления протекания тока. Точке потенциала с максимальным номером соответствует потенциал положительного электрода источника ЭДС. В схеме рис. 3. 10 потенциал изменяется 3 раза, таким образом, отмечаем на схеме 4 точки. Из 0 откладываем вектор напряжения на сопротивлении, который совпадает с током по фазе, и попадаем в точку 1. Конец вектора направлен к большему потенциалу (к точке 1). Из точки 1 откладываем вектор напряжения на индуктивности, он опережает вектор тока на 90. Конец вектора направлен к точке 2. Из точки 2 откладывае

Рис. 3. 12. Пример разветвленной электрической цепи переменного тока

м вектор напряжения на конденсаторе, он отстает от вектора тока на 90 и проводится параллельно вектору с небольшим смещением. Конец вектора направлен к точке 3. После построения диаграммы напряжений на элементах схемы необходимо провести вектор между точками 0 и 3. Конец полученного вектора должен быть направлен в точку 3, амплитуда полученного вектора (в выбранном масштабе напряжений) должна соответствовать действующему значению напряжения источника ЭДС , а фаза равняться ₀.

При расчете разветвленных цепей переменного тока могут применяться любые методы, описанные в пп. 2.3.1 – 2.3.6. Чаще всего применяют метод последовательных преобразований или метод контурных токов. Рассмотрим пример расчета разветвленной цепи переменного тока (рис. 3.12) методом контурных токов. В цепи действует ЭДС

.

Начальная фаза источника ЭДС равна 90, то есть при расчете значение напряжения будет иметь только мнимую составляющую. Уравнения для контурных токов в комплексной форме будут иметь вид

(3. 33)

Из этих уравнений выразим контурные токи, заменив сопротивления всех элементов и источника ЭДС их численными значениями. Здесь приведем решение в общем виде:

Источник