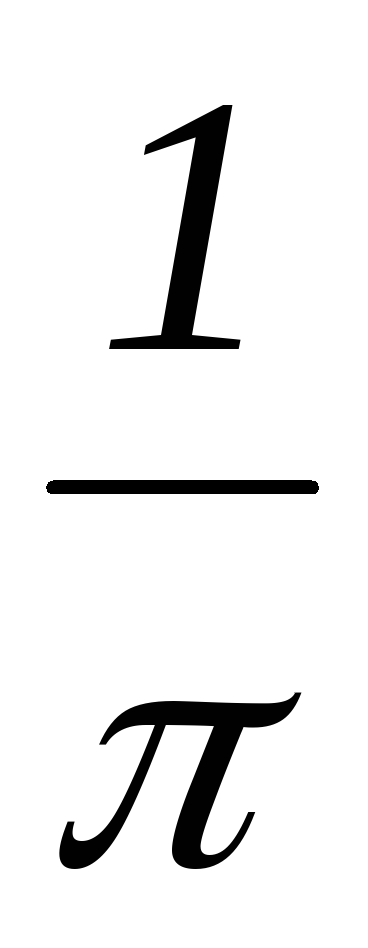
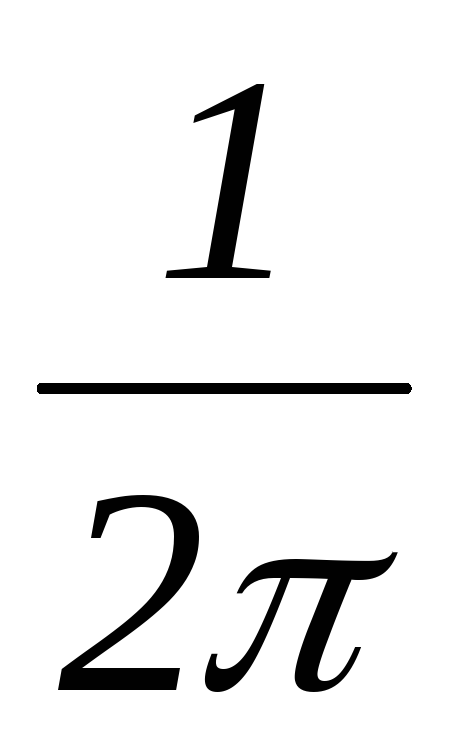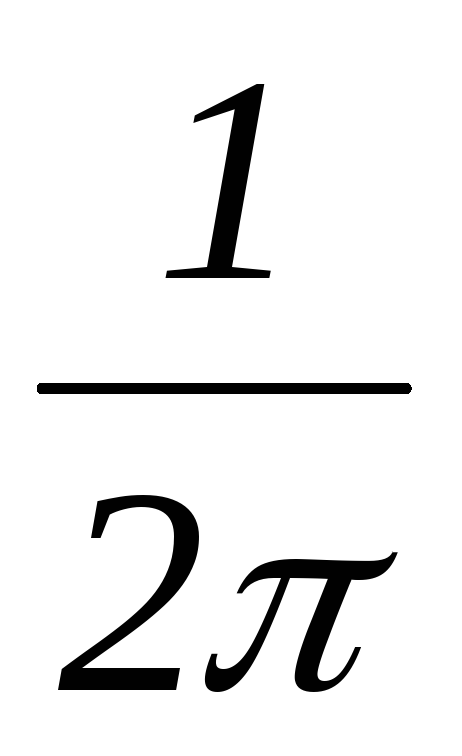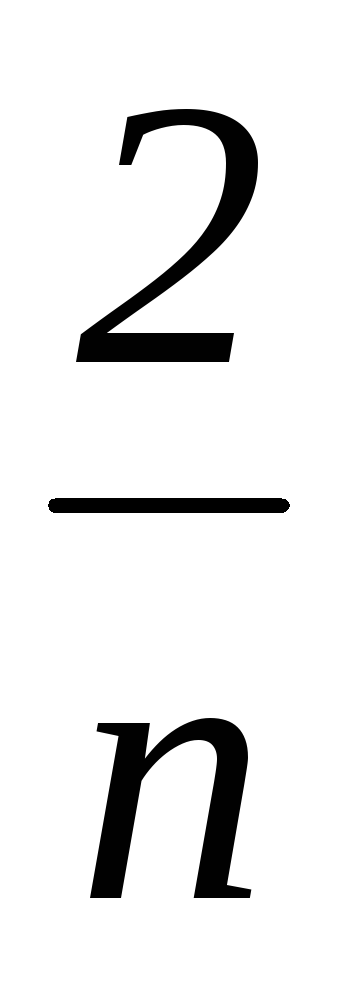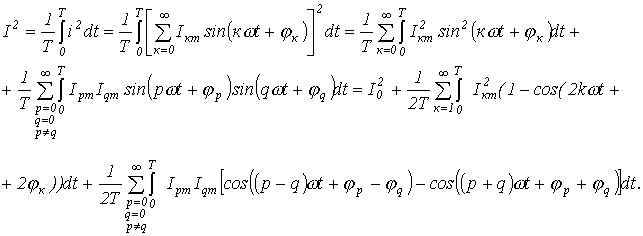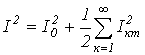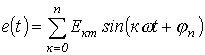Исследование электрических цепей несинусоидального тока
Цель работы: экспериментальная проверка методики расчета линейных электрических цепей при несинусоидальных воздействиях и исследование влияния индуктивности и емкости на форму кривой тока.
Пояснения к работе
Методика расчета линейных электрических цепейнесинусоидального тока состоит в том, что заданное несинусоидальное периодическое напряжение или ток источника аналитически или графоаналитически представляют в виде гармонического ряда Фурье, после чего выполняют расчет цепи по каждой гармонике отдельно и записывают результирующие значения мгновенных или действующих значений токов и напряжений на отдельных участках.
В общем случае периодическая несинусоидальная функция представляется рядом Фурье вида
где A0 — постоянная составляющая ряда Фурье или нулевая гармоника;
Если несинусоидальная периодическая функция f( t) имеет геометрически правильную форму и легко может быть представлена в виде аналитической функции, то ее разложение в ряд Фурье осуществляется аналитически согласно известным формулам. Результаты такого разложения приведены в справочниках.
При произвольной форме функции f( t) ее разложение в ряд Фурье осуществляется графоаналитическим методом. Этот метод основан на замене определенного интеграла суммой конечного числа слагаемых. С этой целью период несинусоидальной функции f( t) разбивают на n равных интервалов t=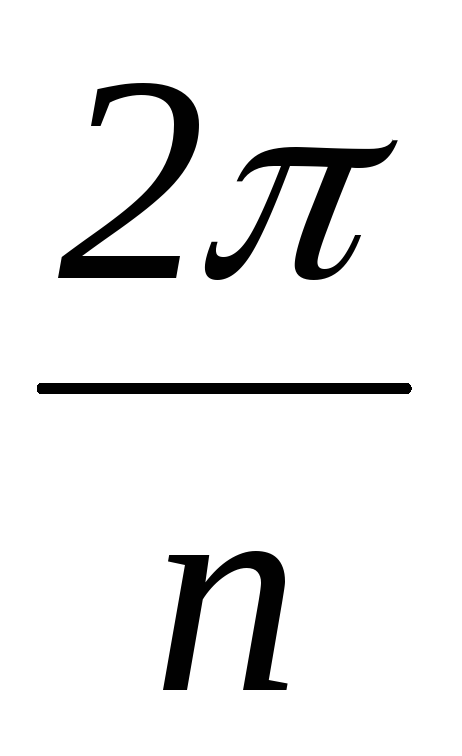
A0 = 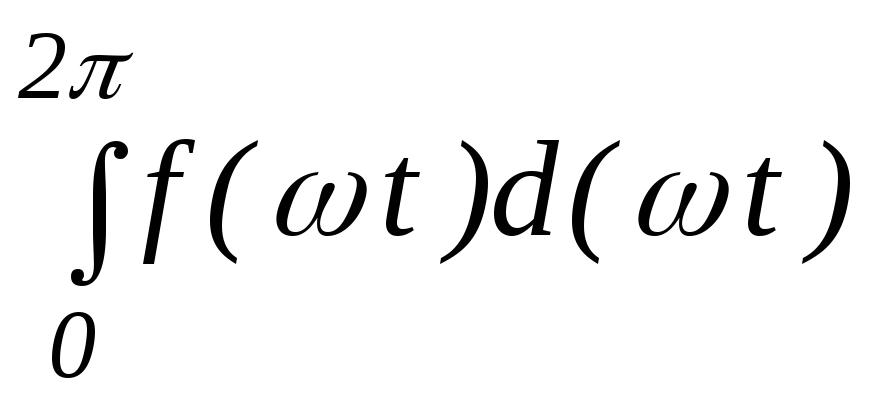
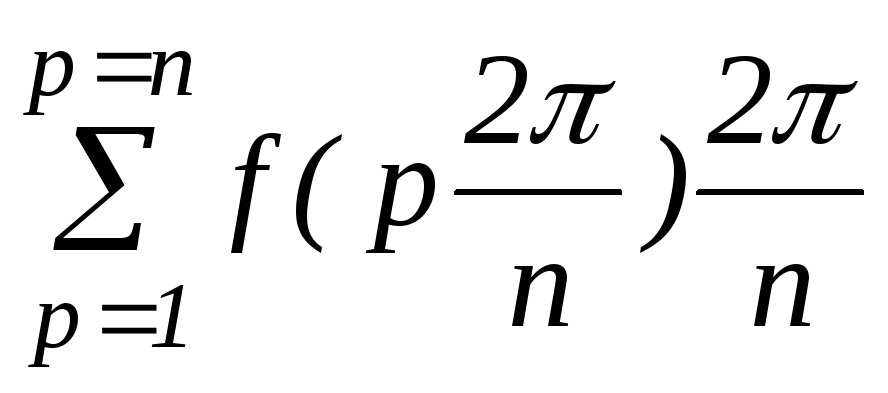
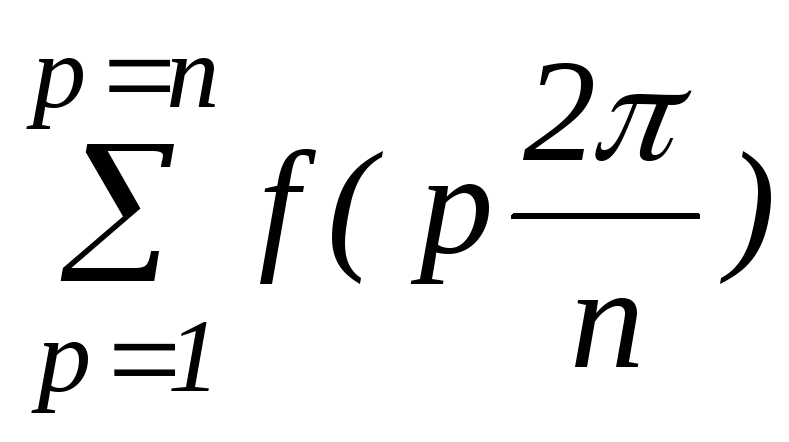
A k = 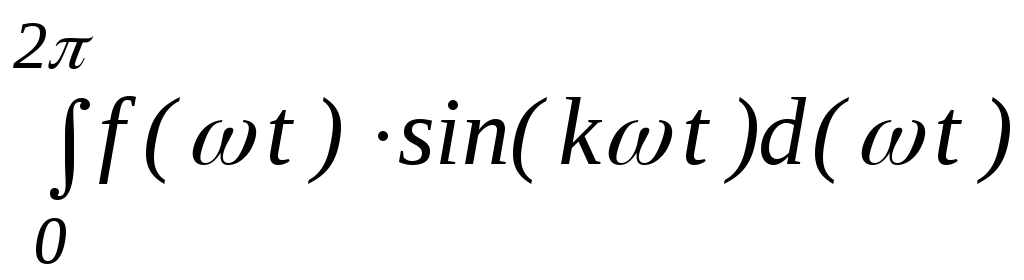
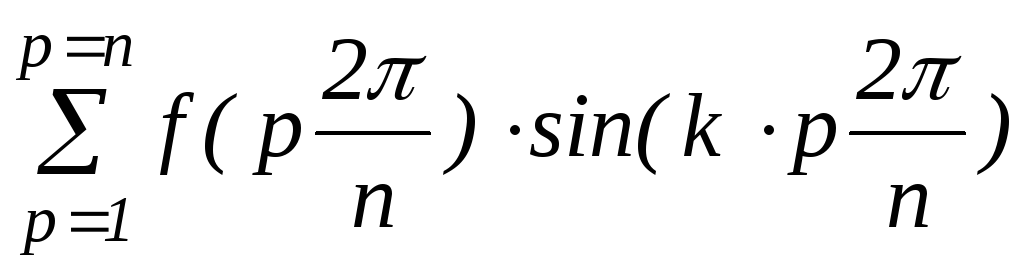
Ak = 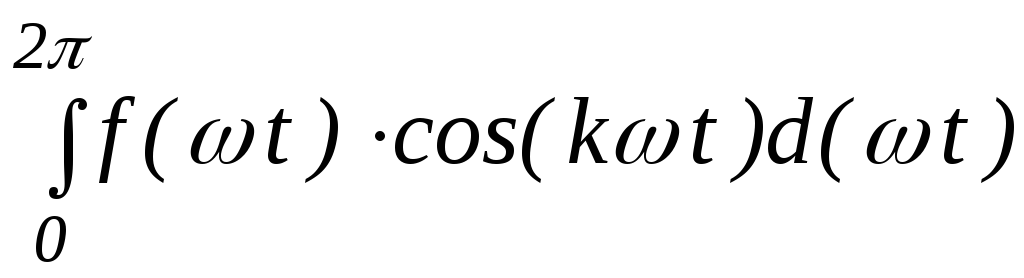
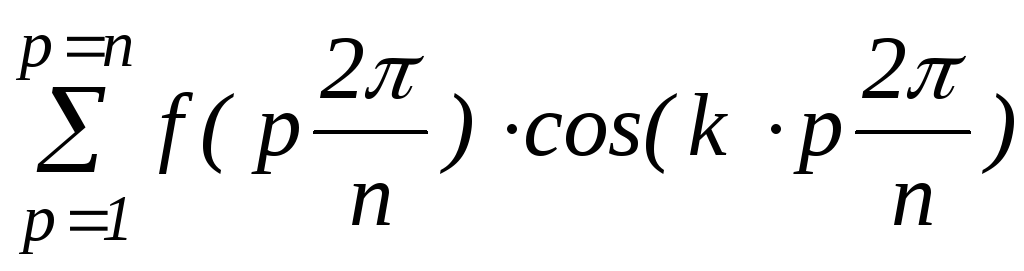
Где: f(p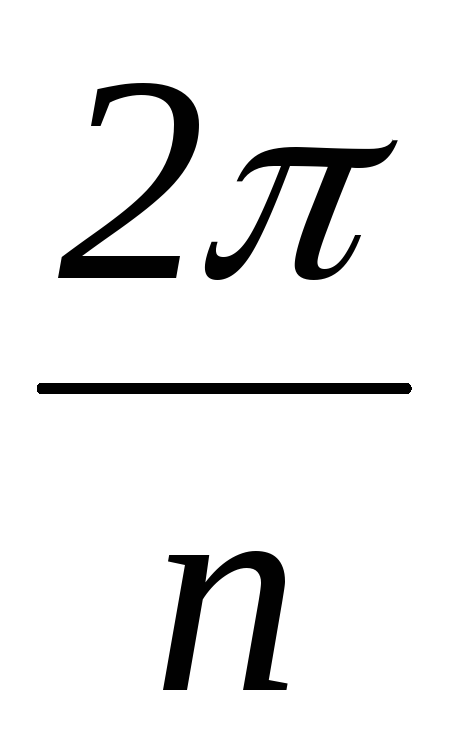
sin(k·p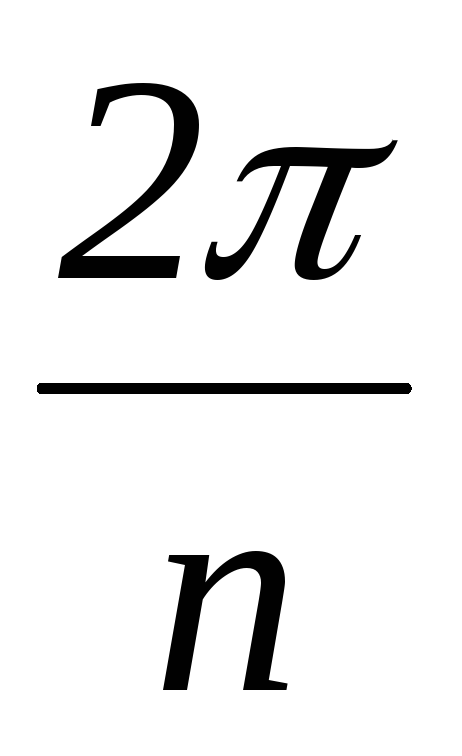
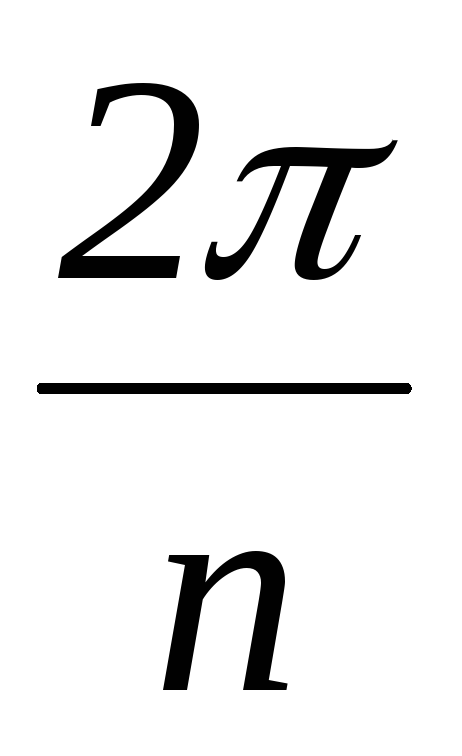
Чем больше число интервалов, тем точнее результат разложения в ряд Фурье. На практике обычно достаточно разделить период на 24 или 18 интервалов.
Если несинусоидальная периодическая кривая симметрична относительно оси абсцисс, то на n равных интервалов разбивают полпериода и по формулам, аналогичным (11.2 – 11.4) находят гармонические составляющие ряда Фурье.
При замене синусного и косинусного рядов одинарным синусоидальным рядом фурье (11.1) используют следующие формулы:
Ak =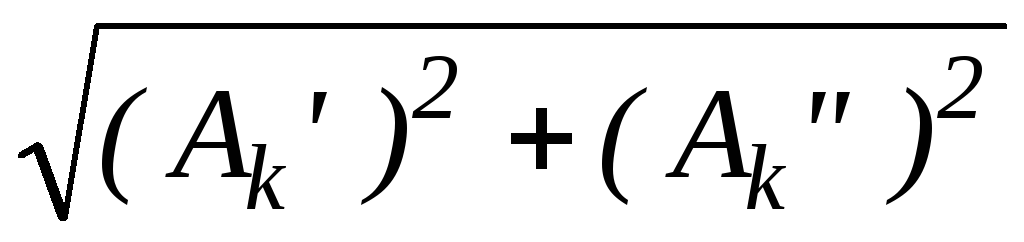
k = arctg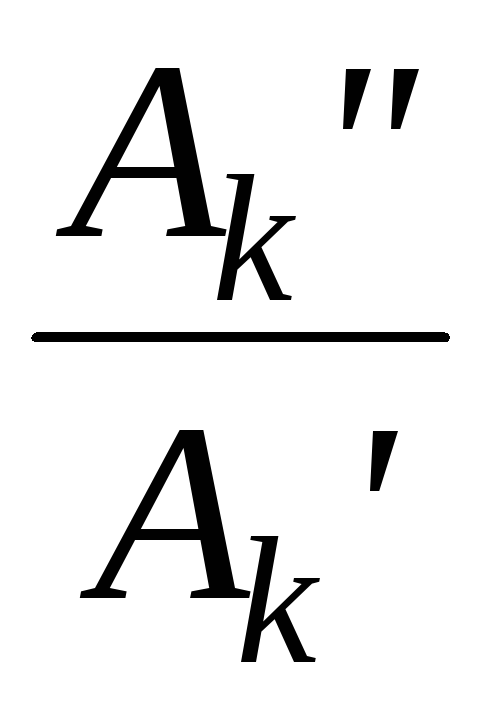
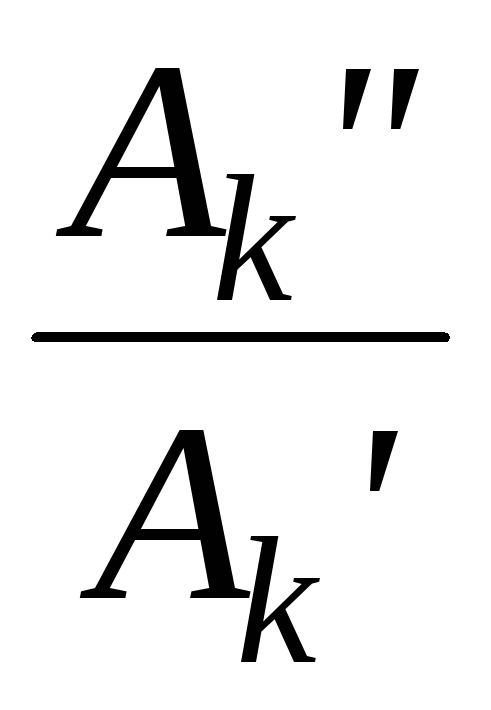
Из приведенных соотношений следует, что индуктивность подавляет высшие гармоники в составе кривой тока, делая ее по форме близкой к виду первой гармоники подаваемого напряжения источника. Емкость, наоборот, способствует увеличению высших гармоник в кривой тока, чем делает ее более искаженной в сравнении с кривой питающего напряжения.
Действующие значения несинусоидальных напряжений и токов:
u =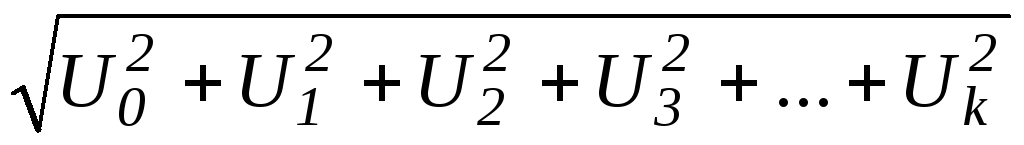
I =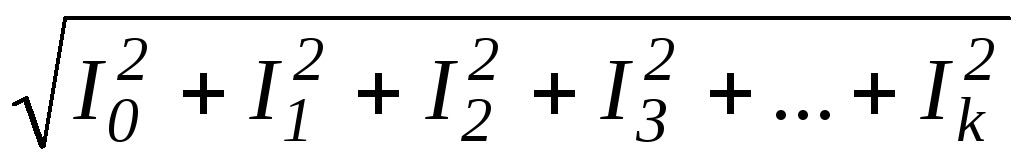
Мгновенное значение несинусоидального тока равно сумме мгновенных значений токов всех гармоник:
Домашняя подготовка к работе
1. Согласно номеру варианта (табл.11.1) вычертить график несинусоидального напряжения источника (рис. 11.1 или 11.2), электрическую цепь для проведения исследований (рис. 11.3) и выбрать их параметры (табл.1).
Таблица 11.1. Параметры электрической цепи для исследований.
Источник
Vse_lekcii_TEMK / Лекция N 22. Линейные электрические цепи при несинусоидальных периодических токах
Предыдущие лекции были посвящены анализу электрических цепей при синусоидальных токах и напряжениях. На практике ЭДС и токи в большей или меньшей степени являются несинусоидальными. Это связано с тем, что реальные генераторы не обеспечивают, строго говоря, синусоидальной формы кривых напряжения, а с другой стороны, наличие нелинейных элементов в цепи обусловливает искажение формы токов даже при синусоидальных ЭДС источников.
На практике к несинусоидальности напряжений и токов следует подходить двояко:
в силовой электроэнергетике несинусоидальные токи обусловливают в общем случае дополнительные потери мощности, пульсации момента на валу двигателей, вызывают помехи в линиях связи; поэтому здесь необходимо «всеми силами» поддержание синусоидальных режимов;
в цепях автоматики и связи, где несинусоидальные токи и напряжения лежат в основе принципа действия электротехнических устройств, задача наоборот заключается в их усилении и передаче с наименьшими искажениями.
В общем случае характер изменения величин может быть периодическим, почти периодическим и непериодическим. В данном разделе будут рассматриваться цепи только с периодическими переменными.
Периодическими несинусоидальными величинами называются переменные, изменяющиеся во времени по периодическому несинусоидальному закону. Причины возникновения несинусоидальных напряжений и токов могут быть обусловлены или несинусоидальностью источника питания или (и) наличием в цепи хотя бы одного нелинейного элемента. Кроме того, в основе появления несинусоидальных токов могут лежать элементы с периодически изменяющимися параметрами.
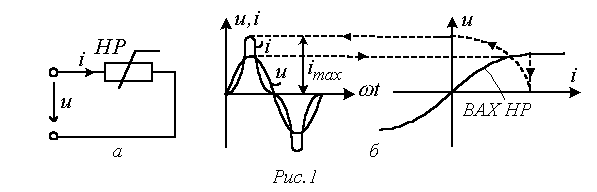
В качестве примера на рис. 1,а представлена цепь с нелинейным резистором (НР), нелинейная вольт-амперная характеристика (ВАХ) которого обусловливает несинусоидальную форму тока i в цепи при синусоидальном напряжении u на ее входе (см. рис. 1,б).
Характеристики несинусоидальных величин
Для характеристики несинусоидальных периодических переменных служат следующие величины и коэффициенты (приведены на примере периодического тока):
Максимальное значение — 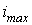
Действующее значение — 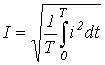
Среднее по модулю значение — 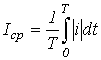
Среднее за период значение (постоянная составляющая) — 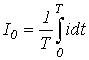
Коэффициент амплитуды (отношение максимального значения к действующему) — 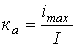
Коэффициент формы (отношение действующего значения к среднему по модулю) — 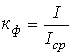
Коэффициент искажений (отношение действующего значения первой гармоники к действующему значению переменной) — 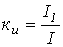
Коэффициент гармоник (отношение действующего значения высших гармонических к действующему значению первой гармоники) — 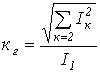
Разложение периодических несинусоидальных кривых в ряд Фурье
Из математики известно, что всякая периодическая функция 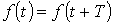
При разложении в ряд Фурье функция представляется следующим образом:
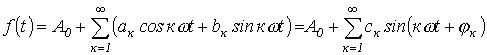
Здесь 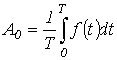
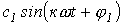
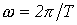
В выражении (1) 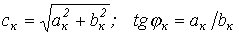
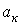
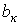
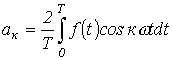
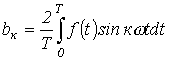
Свойства периодических кривых, обладающих симметрией
Коэффициенты ряда Фурье для стандартных функций могут быть взяты из справочной литературы или в общем случае рассчитаны по приведенным выше формулам. Однако в случае кривых, обладающих симметрией, задача существенно упрощается, поскольку из их разложения выпадают целые спектры гармоник. Знание свойств таких кривых позволяет существенно сэкономить время и ресурсы при вычислениях.
К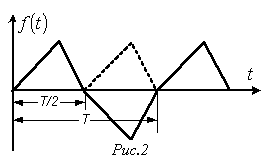
К данному типу относятся кривые, удовлетворяющие равенству 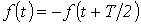
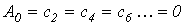
К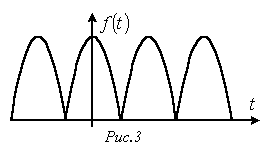
К данному типу относятся кривые, для которых выполняется равенство (см. пример на рис. 3). В их разложении отсутствуют синусные составляющие, т.е.
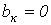
К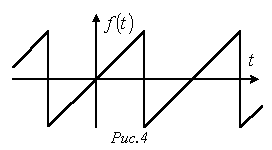
К этому типу относятся кривые, удовлетворяющие равенству 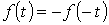
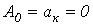
Действующее значение периодической несинусоидальной переменной
Как было показано выше, действующим называется среднеквадратичное за период значение величины:
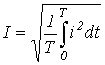
При наличии аналитического выражения функции i(t) и возможности взятия интеграла от ее квадрата действующее значение i(t) определяется точно. Однако в общем случае на практике действующее значение переменной определяется на основе информации о действующих значениях конечного ряда гармонических.
Пусть 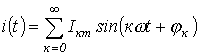
Очевидно, что каждый из интегралов от тригонометрических функций в последнем выражении равен нулю. Таким образом,
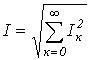
Аналогичные выражения имеют место для ЭДС, напряжения и т.д.
Мощность в цепях периодического несинусоидального тока
Пусть 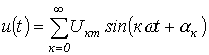
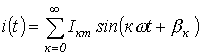
Тогда для активной мощности можно записать
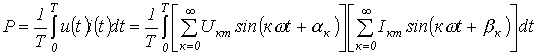
Как было показано при выводе соотношения для действующего значения несинусоидальной переменной, среднее за период значение произведения синусоидальных функций различной частоты равно нулю. Следовательно,
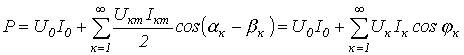
где 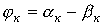
Таким образом, активная мощность несинусоидального тока равна сумме активных мощностей отдельных гармонических:

Аналогично для реактивной мощности можно записать
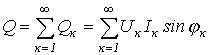
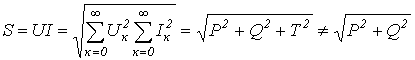
где Т – мощность искажений, определяемая произведениями действующих значений разнопорядковых гармонических тока и напряжения.
Методика расчета линейных цепей при периодических
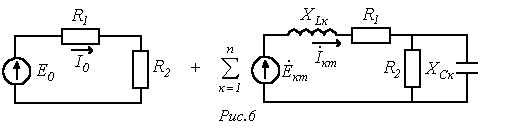
В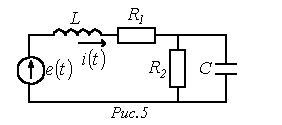
(при расчете спектр рассматриваемых гармоник ограничивается) в расчетном плане представляется суммой цепей на рис. 6.
Здесь 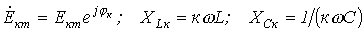
Тогда, например, для тока в ветви с источником ЭДС, имеем
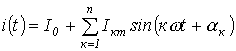
где каждая к-я гармоника тока рассчитывается символическим методом по своей к-й расчетной схеме. При этом (поверхностный эффект не учитывается) для всех гармоник параметры 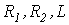
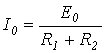
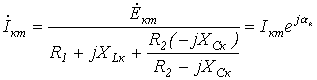
Необходимо помнить, что ввиду различия частот суммировать комплексы различных гармоник недопустимо.
Таким образом, методика расчета линейных цепей при несинусоидальных токах сводится к следующему:
ЭДС и токи источников раскладываются в ряды Фурье.
Осуществляется расчет цепи в отдельности для каждой гармонической.
Искомые величины определяются как алгебраические суммы соответствующих гармонических.
Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
Что является причиной появления несинусоидальных токов и напряжений в электрических цепях?
Какие величины и коэффициенты характеризуют периодические несинусоидальные переменные?
Какие гармонические отсутствуют в спектрах кривых, симметричных относительно: 1) оси абсцисс; 2) оси ординат; 3) начала системы координат?
Достаточно ли для определения величины полной мощности в цепи несинусоидального тока наличие информации об активной и реактивной мощностях?
Для каких цепей справедлива методика расчета цепей несинусоидального тока, основанная на разложении ЭДС и токов источников в ряды Фурье?
Не прибегая к разложению в ряд Фурье, определить коэффициенты амплитуды и формы кривой на рис. 4.
Ответ: 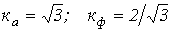
Определить действующее значение напряжения на зажимах ветви с последовательным соединением резистора с 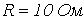
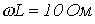
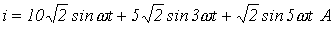
Определить действующее значение тока в ветви с источником ЭДС в схеме на рис. 5, если 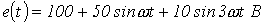
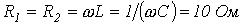
Источник